题目内容
7.同时抛掷两个骰子(各个面上分别标有数字1,2,3,4,5,6),计算:(1)向上的数相同的概率.
(2)向上的数之积为偶数的概率.
分析 (1)每掷1个骰子都有6种情况,所以同时掷两个骰子总的结果数为6×6=36.向上的数相同的结果有6种,由此能求出向上的数相同的概率.
(2)向上的数之积为偶数的情况比较多,可以先考虑其对立事件,即向上的数之积为奇数.利用列举法求出向上的数之积为奇数的基本事件个数,由此利用对立事件概率计算公式能求出向上的数之积为偶数的概率.
解答 解:(1)每掷1个骰子都有6种情况,所以同时掷两个骰子总的结果数为6×6=36.
向上的数相同的结果有6种,故向上的数相同的概率为P(A)=$\frac{6}{36}$=$\frac{1}{6}$.
(2)向上的数之积为偶数的情况比较多,可以先考虑其对立事件,即向上的数之积为奇数.
向上的数之积为奇数的基本事件有:
(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9个,
故向上的数之积为偶数的概率为P(B)=1-$\frac{9}{36}$=1-$\frac{1}{4}$=$\frac{3}{4}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
17.已知O是△ABC中的一点,$\overrightarrow{OA}$+3$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow 0$,则△OAB与△OAC的面积之比为( )
| A. | 1:3 | B. | 1 | C. | 5:3 | D. | 3:5 |
17.三次函数$f(x)=a{x^3}-\frac{3}{2}{x^2}+2x+1$的图象在点(1,f(1))处的切线与x轴平行,则f(x)在区间(1,3)上的最小值是( )
| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
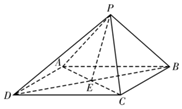 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.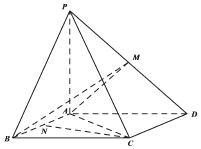 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.