题目内容
设函数f(x)=|2x-4|+1.

(1)画出函数y=f(x)的图象;
(2)若不等式f(x)≤ax的解集非空,求a的取值范围.
解析:(1)由于f(x)= 则函数y=f(x)的图象如图所示.
则函数y=f(x)的图象如图所示.

(2)由函数y=f(x)与函数y=ax的图象可知,当且仅当a≥ 或a<-2时,函数y=f(x)与函数y=ax的图象有交点.
或a<-2时,函数y=f(x)与函数y=ax的图象有交点.
故不等式f(x)≤ax的解集非空时,a的取值范围为(-∞,-2)∪ .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目

 时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f
时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f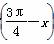 是( )
是( )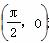 对称
对称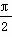 对称
对称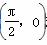 对称
对称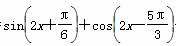 +sin 2x,x∈[0,π].
+sin 2x,x∈[0,π].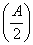 =
=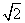 ,a=2,b=
,a=2,b=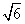 ,求角C.
,求角C.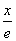 +
+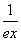 (e≈2.718…).
(e≈2.718…).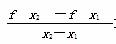 >0;
>0;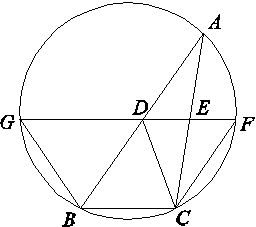
 =________.
=________.