题目内容
已知x=
(p
-p-
),n∈N*,p>0,求
的值.
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
(x+
| ||
| p |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:由x=
(p
-p-
),n∈N*,p>0.可得x2+1=[
(p
+p-
)]2,再利用指数幂的运算法则即可得出.
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
解答:
解:∵x=
(p
-p-
),n∈N*,p>0.
∴x2+1=
(p
+p-
-2)+1=[
(p
+p-
)]2,
∴x+
=p
.
∴
=
=
=1.
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
∴x2+1=
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
∴x+
| 1+x2 |
| 1 |
| n |
∴
(x+
| ||
| p |
(p
| ||
| p |
| p |
| p |
点评:本题考查了指数幂的运算法则及其乘法公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知f(x)=
则f(2)-f(-2)的值为( )
|
| A、6 | B、5 | C、4 | D、2 |
函数y=-x3-x2+2的极值情况是( )
| A、有极大值,无极小值 |
| B、有极小值,无极大值 |
| C、既无极大值也无极小值 |
| D、既有极大值又有极小值 |
数列{-2n2+29n+3}中最大项是( )
| A、107 | ||
| B、108 | ||
C、108
| ||
| D、109 |
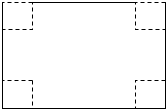 如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为