题目内容
12.曲线y=e${\;}^{\frac{1}{3}x}$在点(6,e2)处的切线与坐标轴所围成的三角形的面积为( )| A. | $\frac{3}{2}{e}^{2}$ | B. | 3e2 | C. | 6e2 | D. | 9e2 |
分析 求出函数的导数,求得切线的斜率,由点斜式方程可得切线的方程,分别令x=0,y=0求得与y,x轴的交点,运用三角形的面积公式计算即可得到所求值.
解答 解:y=e${\;}^{\frac{1}{3}x}$的导数为y′=$\frac{1}{3}$e${\;}^{\frac{1}{3}x}$,
可得在点(6,e2)处的切线斜率为$\frac{1}{3}$e2,
即有在点(6,e2)处的切线方程为y-e2=$\frac{1}{3}$e2(x-6),
即为y=$\frac{1}{3}$e2x-e2,
令x=0,可得y=-e2;令y=0,可得x=3.
即有切线与坐标轴所围成的三角形的面积为$\frac{1}{2}$•3•e2=$\frac{3}{2}$e2.
故选:A.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用直线方程是解题的关键,属于基础题.

练习册系列答案
相关题目
17.某单位共有职工150名,其中高级职称45人,中级职称90人,初级职称15人.现采用分层抽样方法从中抽取容量为30的样本,则各职称人数分别为( )
| A. | 9,18,3 | B. | 10,15,5 | C. | 10,17,3 | D. | 9,16,5 |
4.某程序框图如图所示,若输入p=2,则输出的结果是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
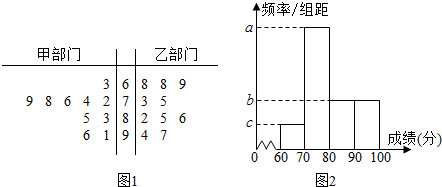
 长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).