题目内容
若a,b∈{-1,0,1,2},则函数f(x)=ax2+2x+b有零点的概率为 A( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:列举可得总的方法种数为16,其中满足f(x)=ax2+2x+b有零点的有13个,由概率公式可得.
解答:
解:∵a,b∈{-1,0,1,2},
∴列举可得总的方法种数为:
(-1,-1),(-1,0),(-1,1),(-1,2),
(0,-1),(0,0),(0,1),(0,2),
(1,-1),(1,0),(1,1),(1,2),
(2,-1),(2,0),(2,1),(2,2)共16个,
其中满足f(x)=ax2+2x+b有零点的为:
(-1,-1),(-1,0),(-1,1),(-1,2),
(0,-1),(0,0),(0,1),(0,2),
(1,-1),(1,0),(1,1),(2,-1),(2,0)共13个
∴所求概率P=
故选:A
∴列举可得总的方法种数为:
(-1,-1),(-1,0),(-1,1),(-1,2),
(0,-1),(0,0),(0,1),(0,2),
(1,-1),(1,0),(1,1),(1,2),
(2,-1),(2,0),(2,1),(2,2)共16个,
其中满足f(x)=ax2+2x+b有零点的为:
(-1,-1),(-1,0),(-1,1),(-1,2),
(0,-1),(0,0),(0,1),(0,2),
(1,-1),(1,0),(1,1),(2,-1),(2,0)共13个
∴所求概率P=
| 13 |
| 16 |
故选:A
点评:本题考查列举法计算基本事件数以及概率公式,属基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
若椭圆的中心在原点,一个焦点为(0,2),直线y=3x+7与椭圆相交所得弦的中点的纵坐标为1,则这个椭圆的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从装有2个黄球和2个蓝球的口袋内任取2个球,则恰有一个黄球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2在下列哪个区间存在零点( )
| A、(-3,-1) |
| B、(-1,2) |
| C、(2,3) |
| D、(3,4) |
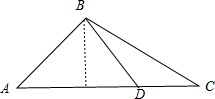 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.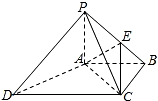 四棱锥P-ABCD中,DC∥AB,AB=2DC=4
四棱锥P-ABCD中,DC∥AB,AB=2DC=4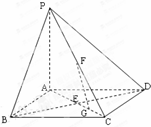 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.