题目内容

在三维直角坐标系中，已知A（1，1，1），B（2，2，2），C（3，2，4），求△ABC的面积S△ABC．
考点：三角形的面积公式
专题：空间向量及应用
分析：利用向量的夹角公式可得cosA，利用平方关系可得sinA，再利用三角形的面积计算公式即可得出．
解答： 解：
AB
=（1，1，1），
AC
=（2，1，3），
∴
AB
•
AC
=2+1+3=6，|
AB
|=
3
，|
AC
|=
14
．
∴cosA=
AB
•
AC
|
AB
||
AC
|
=
6
3
×
14
=
14
7
．
∴sinA=
1-cos2A
=
35
7
．
∴S△ABC=
1
2
|
AB
||
AC
|sinA=
1
2
×
3
×
14
×
14
7
=
3
．
点评：本题考查了向量的夹角公式、同角三角函数的平方关系、三角形的面积计算公式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
求下列各式的值：
（1）（2
1
4
） 
1
2
-（9.6）0-（3
3
8
） -
2
3
+（1
1
2
）-2
（2）log3
1
3
+lg25+lg4+7 log72．
莆田往福州的某次动车途中经停福清站，为了方便莆田市VIP客户搭乘，车站信息管理员对该次动车VIP车厢（共4个座位）莆田至福州的全程空座位数n进行统计，得到10个车次样本数据的茎叶图，如图所示．（全程空座位数即莆田至福清、福清至福州两个站段的空座位数之和）
（1）求样本平均数
.
n
；
（2）某天，VIP客户李明因有急事凭身份证从莆田搭乘该次动车，补买VIP车厢无座票（没有座位，若有空座位则可就坐）前往福州，且途中不再更换车厢，若以样本平均数
.
n
估计该次动车VIP车厢的全程空座位数，且在两个站段共8个座位中，每个座位成为空座位数是等可能的．
①将VIP车厢第i号座位在莆田至福清站段标记为ai，在福清至福州站段标记为bi（i=1，2，3，4），请列举出途中出现
.
n
个空座位所有的可能结果；
②求李明在途中恰有一个站段有座位坐的概率．
求函数f（x）=x2-2ax在x∈[-1，1]上的最小值．
如图，PA是圆O的切线，A为切点，PO与圆O交于点B、C，AQ⊥OP，垂足为Q．若PA=4，PC=2，求AQ的长．
对任意x、y，f（x）满足f（x+y）=f（x）+f（y）且当x＞0时，f（x）＜0，又f（1）=-2．
（1）求证：f（x）是R上的减函数；
（2）若?x∈R，不等式f（ax2）-2f（x）＜f（x）+4恒成立，求a的取值范围．
已知函数f（x）=lg（x2-2x+m），其中m∈R，且m为常数．
（1）求这个函数的定义域； 
（2）函数f（x）的定义域与值域能否同时为实数集R？证明你的结论．
（3）函数f（x）的图象有无平行于y轴的对称轴？证明你的结论．
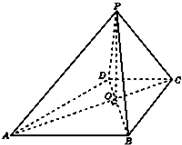如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC，AC⊥BD，AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2，PO=
2
，PB⊥PD．
（Ⅰ）求异面直线PD与BC所成角的余弦值；
（Ⅱ）求二面角P-AB-C的大小．
函数y=|x|的单调减区间为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网