题目内容
8.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1,|{\overrightarrow a-2\overrightarrow b}|≤2$,则$\overrightarrow b$在$\overrightarrow a$上的投影的取值范围是( )| A. | $[{\frac{1}{2},2}]$ | B. | $({\frac{1}{2},2})$ | C. | $[{\frac{1}{2},1}]$ | D. | $({\frac{1}{2},1})$ |
分析 根据条件可求出$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$cos<\overrightarrow{a},\overrightarrow{b}>$,并且对$|\overrightarrow{a}-2\overrightarrow{b}|≤2$两边平方,进行数量积的运算便可得出cos$<\overrightarrow{a},\overrightarrow{b}>$的取值范围,即得出$\overrightarrow{b}$在$\overrightarrow{a}$上的投影的取值范围.
解答 解:$\overrightarrow{b}$在$\overrightarrow{a}$上的投影为:$|\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$=$cos<\overrightarrow{a},\overrightarrow{b}>$;
由$|\overrightarrow{a}|=2,|\overrightarrow{b}|=1$,对$|\overrightarrow{a}-2\overrightarrow{b}|≤2$两边平方得:
${\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}=4-8cos<\overrightarrow{a},\overrightarrow{b}>+4≤4$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>≥\frac{1}{2}$;
∴$\frac{1}{2}≤cos<\overrightarrow{a},\overrightarrow{b}>≤1$;
即$\frac{1}{2}≤|\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>≤1$;
∴$\overrightarrow{b}$在$\overrightarrow{a}$上的投影的取值范围是$[\frac{1}{2},1]$.
故选:C.
点评 考查一个向量在另一个向量方向上投影的定义及计算公式,向量数量积的运算及计算公式,以及不等式的性质.

| A. | 其图象关于直线x=-$\frac{π}{4}$对称 | B. | 函数g(x)是奇函数 | ||
| C. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | D. | x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,0)∪(1,+∞) |
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$或$\sqrt{6}$ | D. | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ |
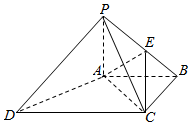 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.