题目内容
13.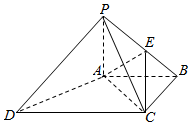 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.(1)PD∥平面EAC.
(2)求平面ACE分四棱锥两部分E-ABC与PE-ACD的体积比.
分析 (1)利用线面垂直的性质,可得在直角梯形ABCD中AC⊥AD,根据题中数据结合平行线分线段成比例,算出DC=2AB,从而得到△BPD中,PE:EB=DM:MB=2,所以PD∥EM,由线面平行的判定定理可得PD∥平面EAC.
(2)求出三棱锥E-ABC与四棱锥P-ABCD的体积比,即可求出平面ACE分四棱锥两部分E-ABC与PE-ACD的体积比.
解答 (1)证明:∵PC⊥AD,
∴在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=$\frac{π}{4}$,
∴∠DCA=∠BAC=$\frac{π}{4}$,
又AC⊥AD,故△DAC为等腰直角三角形,
∴DC=$\sqrt{2}$AC=2AB.
连接BD,交AC于点M,则$\frac{DM}{MB}$=$\frac{DC}{AB}$=2.
连接EM,在△BPD中,$\frac{PE}{EB}$=$\frac{DM}{MB}$=2,∴PD∥EM,
又PD?/平面EAC,EM?平面EAC,
∴PD∥平面EAC;
(2)解:由PE=2EB知三棱锥E-ABC的高是四棱锥P-ABCD的高的$\frac{1}{3}$.
△ABC的面积为$\frac{1}{2}$,四边形ABCD的面积为$\frac{1}{2}+1=\frac{3}{2}$,
∴三棱锥E-ABC与四棱锥P-ABCD的体积比为$\frac{1}{9}$,
∴平面ACE分四棱锥两部分E-ABC与PE-ACD的体积比为$\frac{1}{8}$.
点评 本题给出底面是直角梯形的四棱锥,求证线面平行和平面ACE分四棱锥两部分E-ABC与PE-ACD的体积比.着重考查了空间线面平行的判定定理,考查体积的计算等知识,属于中档题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
1.已知复数z=1+i(i是虚数单位),则$\frac{2}{z}$-z2的共轭复数是( )
| A. | -1+3i | B. | 1+3i | C. | 1-3i | D. | -1-3i |
8.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1,|{\overrightarrow a-2\overrightarrow b}|≤2$,则$\overrightarrow b$在$\overrightarrow a$上的投影的取值范围是( )
| A. | $[{\frac{1}{2},2}]$ | B. | $({\frac{1}{2},2})$ | C. | $[{\frac{1}{2},1}]$ | D. | $({\frac{1}{2},1})$ |
5.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=20x的焦点重合,且其渐近线方程为y=±$\frac{4}{3}$x,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{64}$=1 | D. | $\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1 |
2.已知双曲线的一条渐近线方程为y=4x,且双曲线的焦点与抛物线y2=8x的焦点是重合的,则双曲线的标准方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{{17{x^2}}}{4}-\frac{{17{y^2}}}{64}=1$ | ||
| C. | $\frac{x^2}{4}-\frac{{4{y^2}}}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程$y=\sqrt{3}x$,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |