题目内容
18.双曲线C的渐近线方程为y=±$\sqrt{2}$x,则C的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$或$\sqrt{6}$ | D. | $\sqrt{3}$或$\frac{\sqrt{6}}{2}$ |
分析 由双曲线的渐近线的方程可得$\frac{b}{a}$=$\sqrt{2}$,或$\frac{a}{b}$=$\sqrt{2}$,再利用c2=a2+b2,将所得等式转化为关于离心率的方程即可解得离心率
解答 解:设双曲线的实轴长为2a,虚轴长为2b,焦距为2c,则c2=a2+b2,e=$\frac{c}{a}$
∵双曲线的渐近线为y=±$\sqrt{2}$x
∴$\frac{b}{a}$=$\sqrt{2}$,或$\frac{a}{b}$=$\sqrt{2}$
∴$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}$=2或$\frac{{a}^{2}}{{c}^{2}{-a}^{2}}$=2
∴c2=3a2或2c2=3a2
∴e2=3或e2=$\frac{3}{2}$
∴e=$\sqrt{3}$或e=$\frac{\sqrt{6}}{2}$
故选:D
点评 本题考查了双曲线的几何性质,双曲线的渐近线方程的意义以及双曲线离心率的求法.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
8.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1,|{\overrightarrow a-2\overrightarrow b}|≤2$,则$\overrightarrow b$在$\overrightarrow a$上的投影的取值范围是( )
| A. | $[{\frac{1}{2},2}]$ | B. | $({\frac{1}{2},2})$ | C. | $[{\frac{1}{2},1}]$ | D. | $({\frac{1}{2},1})$ |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程$y=\sqrt{3}x$,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
8.若tanα=3,tanβ=$\frac{4}{3}$,则$\frac{1}{tan(α-β)}$等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
 已知四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA⊥底面ABCD,M为AB的中点.
已知四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA⊥底面ABCD,M为AB的中点.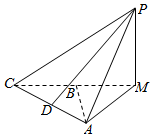 如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.
如图,在三棱锥P-AMC中,AC=AM=PM=2,PM⊥面AMC,AM⊥AC,B,D分别为CM,AC的中点.