题目内容
10.$\underset{∬}{D}$$\frac{y}{{x}^{2}+{y}^{2}}$dσ,D是由y2=x,y=x及y=$\sqrt{3}$围成的区域.分析 根据二重积分的性质和法则计算即可.
解答 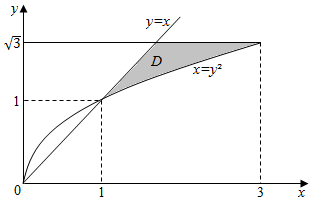 解:由$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,由$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=\sqrt{3}}\end{array}\right.$,
解:由$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,由$\left\{\begin{array}{l}{{y}^{2}=x}\\{y=\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=\sqrt{3}}\end{array}\right.$,
∴$\underset{∬}{D}$$\frac{y}{{x}^{2}+{y}^{2}}$dσ=${∫}_{1}^{\sqrt{3}}$dy${∫}_{y}^{{y}^{2}}$$\frac{y}{{x}^{2}+{y}^{2}}$dx=$\frac{\sqrt{3}π}{12}$-$\frac{1}{2}$ln2
点评 本题考查了二重积分的性质和计算,属于基础题.

练习册系列答案
相关题目
20.执行如图的程序框图,则输出的S的值为( )
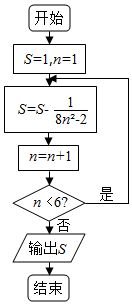

| A. | $\frac{7}{9}$ | B. | $\frac{17}{22}$ | C. | $\frac{10}{13}$ | D. | $\frac{23}{30}$ |
15.已知p:函数f(x)=$\frac{{\sqrt{4-{x^2}}}}{x+4}$-m有零点,q:|m|≤$\frac{{\sqrt{3}}}{3}$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AB,点M、N分别是线段A1C1,A1B的中点.