题目内容
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意x∈[a,a+2],不等式f(x+a)≥f(3x+1)恒成立,则实数a的取值范围是 ________ .
(﹣∞,﹣5].
【解析】∵当x≥0时,f(x)=x2,
∴此时函数f(x)单调递增,
∵f(x)是定义在R上的奇函数,
∴函数f(x)在R上单调递增,
若对任意x∈[a,a+2],不等式f(x+a)≥f(3x+1)恒成立,
则x+a≥3x+1恒成立,
即a≥2x+1恒成立,
∵x∈[a,a+2],
∴(2x+1)max=2(a+2)+1=2a+5,
即a≥2a+5,
解得a≤﹣5,
即实数a的取值范围是(﹣∞,﹣5];
故答案为:(﹣∞,﹣5];

练习册系列答案
相关题目
 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数的取值范围为( )
恒成立,则实数的取值范围为( ) ,
, ,则“
,则“ ”是“
”是“ ∥
∥ ”的( )
”的( ) ,则复数
,则复数 在复平面上对应的点位于
在复平面上对应的点位于 的焦点F与双曲
的焦点F与双曲 的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且
的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且 ,则A点的横坐标为
,则A点的横坐标为 (B)3 (C)
(B)3 (C) (D)4
(D)4 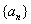 的前
的前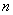 项和为
项和为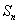 ,点
,点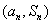 在直线
在直线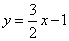 上.
上.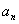 与
与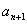 之间插入
之间插入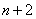 个数组成公差为
个数组成公差为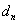 的等差数列,
的等差数列,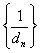 的前
的前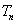 ,并求使
,并求使 成立的正整数
成立的正整数 :
: ,
, :
: .若
.若 .
. 的两焦点分别为
的两焦点分别为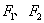 ,
,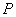 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足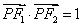 ,过
,过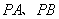 分别交椭圆于
分别交椭圆于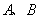 两点. (1)求
两点. (1)求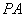 经过点
经过点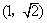 时,求直线
时,求直线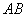 的方程;(3)求证直线
的方程;(3)求证直线 的侧棱
的侧棱 上各有一个动点P、
上各有一个动点P、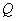 ,且满足
,且满足 ,M是棱CA上的动点,则
,M是棱CA上的动点,则 的最大值是 .
的最大值是 .