题目内容
已知椭圆 的两焦点分别为
的两焦点分别为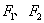 ,
,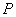 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足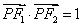 ,过
,过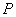 作倾斜角互补的两条直线
作倾斜角互补的两条直线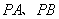 分别交椭圆于
分别交椭圆于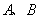 两点. (1)求
两点. (1)求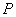 点坐标;(2)当直线
点坐标;(2)当直线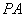 经过点
经过点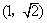 时,求直线
时,求直线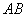 的方程;(3)求证直线
的方程;(3)求证直线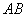 的斜率为定值.
的斜率为定值.
[解](1)由题可得 ,
, ,设
,设 则
则 ,
, ,∴
,∴ ,(1分)∵点
,(1分)∵点 在曲线上,则
在曲线上,则 ,(2分)解得点
,(2分)解得点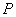 的坐标为
的坐标为 . (4分)
. (4分)
(2)当直线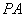 经过点
经过点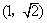 时,则
时,则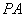 的斜率为
的斜率为 ,因两条直线
,因两条直线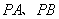 的倾斜角互补,故
的倾斜角互补,故 的斜率为
的斜率为 ,
,
由 得,
得,
即 ,故
,故 ,(2分)同理得
,(2分)同理得 ,
, (4分)
(4分)
∴直线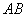 的方程为
的方程为 (6分)
(6分)
(3) 依题意,直线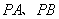 的斜率必存在,不妨设
的斜率必存在,不妨设 的方程为:
的方程为:
 .由
.由 得
得
 ,(2分)设
,(2分)设 ,则
,则
 ,
, ,同理
,同理 ,
,
则 ,同理
,同理 .(4分)
.(4分)
所以: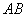 的斜率
的斜率 为定值. (6分)
为定值. (6分)

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
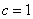 ,且△ABC为锐角三角形,求△ABC的面积的最大值.
,且△ABC为锐角三角形,求△ABC的面积的最大值. 满足
满足 ,则
,则 的最小值是 .
的最小值是 . ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当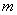 ※
※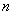 =
=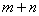 ;当
;当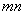 。则在此定义下,集合
。则在此定义下,集合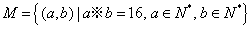 中的元素个数是
中的元素个数是  在定义域内是增函数,则实数
在定义域内是增函数,则实数 的取值范围是 .
的取值范围是 . =
= ,
, =
= ,则
,则 是
是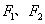 为椭圆
为椭圆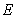 的左右焦点,点
的左右焦点,点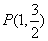 为其上一点,且有
为其上一点,且有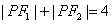
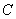 的标准方程;
的标准方程;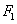 的直线
的直线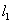 与椭圆
与椭圆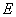 交于
交于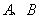 两点,过
两点,过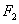 与
与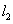 与椭圆
与椭圆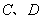 两点,求四边形
两点,求四边形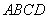 的面积
的面积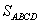 的最大值.
的最大值.