题目内容
设数列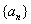 的前
的前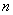 项和为
项和为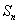 ,点
,点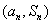 在直线
在直线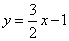 上.
上.
(Ⅰ)求数列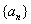 的通项公式;
的通项公式;
(Ⅱ)在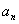 与
与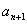 之间插入
之间插入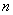 个数,使这
个数,使这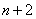 个数组成公差为
个数组成公差为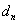 的等差数列,
的等差数列,
求数列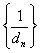 的前
的前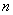 项和
项和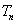 ,并求使
,并求使 成立的正整数
成立的正整数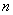 的最大值.
的最大值.
【解析】(Ⅰ)由题设知, ……………………………1分
……………………………1分
得 ),………………………………2分
),………………………………2分
两式相减得: ,
,
即 ,………………………………4分
,………………………………4分
又 得
得 ,
,
所以数列 是首项为2,公比为3的等比数列,
是首项为2,公比为3的等比数列,
∴ . …………………………6分
. …………………………6分
(Ⅱ)由(Ⅰ)知 ,
,
因为 , 所以
, 所以
所以 ……………………8分
……………………8分
令 …
… ,
,
则 …
… ①
①
 …
… ②
②
①…②得 …
… ……………10分
……………10分

 …………………………………11分
…………………………………11分
所以 ,即
,即 ,
,
得
所以,使 成立的正整数
成立的正整数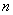 的最大值为
的最大值为 ……………………12分
……………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
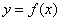 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有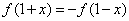 .当
.当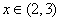 时,
时,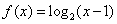
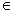 Z)成中心对称;
Z)成中心对称; 是以2为周期的周期函数;
是以2为周期的周期函数; 时,
时,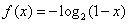 ;
;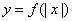 在(k,k+1)( k
在(k,k+1)( k
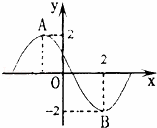
 中,
中, ,
, ,则
,则 .
. 满足
满足 ,则
,则 的最小值是 .
的最小值是 .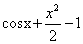
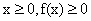 ;
;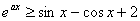 对任意的
对任意的 恒成立,求实数
恒成立,求实数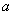 的取值范围.
的取值范围.