题目内容

已知等差数列{an}满足a2+a8+a14+a20=20，若am=5，则m为（　　）
A、11B、12C、22D、44
考点：等差数列的性质,等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质结合a2+a8+a14+a20=20求得a11=5，再由am=5求得m的值．
解答： 解：在差数列{an}中，由a2+a8+a14+a20=20，得：
4a11=20，即a11=5．
又am=5，
∴m=11．
故选：A．
点评：本题考查了等差数列的性质，在等差数列中，若m，n，p，q，k∈N*，且m+n=P+q=2k，则am+an=ap+aq=2ak，是基础题．
练习册系列答案
相关题目
∫
2
0
（2x+5）dx=
 
．
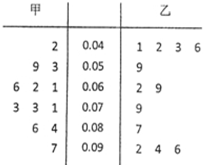PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，如图是根据某地某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，则甲、乙两地浓度的方差较小的是
 
．
已知一扇形的弧长和弧所对的圆心角都是5，则其面积是
 
．
已知an=
∫
n
0
（2x+1）dx，数列{
1
an
}的前n项和为Sn，数列{bn}的通项公式为bn=n+8，则bn•Sn的最小值为
 
．
一个三角形的三个内角A，B，C的度数成等差数列，则B的度数为（　　）
A、30°B、45°
C、60°D、90°
给出以下四个说法：
①若p或q为真命题，则p且q为真命题；
②在刻画回归模型的拟合效果时，相关指数R2的值越大，说明拟合的效果越好；
③在回归直线方程
y
=0.2x+12中，当解释变量x每增加一个单位时，预报变量
y
平均增加0.2个单位；
④对分类变量X与Y，若它们的随机变量K2的观测值k越小，则判断“X与Y有关系”的把握程度越大．
其中正确的说法是 （　　）
A、①④B、②④C、①③D、②③
若x＞0，y＞0，则
x+y
x
+
y
的最小值为（　　）
A、
2
B、1
C、
2
2
D、
1
2
设随机变量的分布列如下表所示，且a+2b=1.3，则a-b=（　　）
X 0 1 2 3
P 0.1 a b 0.1
A、0.5B、0.3
C、0.2D、-0.2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网