题目内容
12.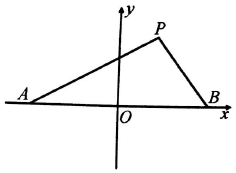 如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.
如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.(1)求P的轨迹方程;
(2)设点P的轨迹为C,点M、N是轨迹为C上不同于A,B的两点,且满足AP∥OM,BP∥ON,求证:△MON的面积为定值.
分析 (1)由题意知$\frac{y}{x+\sqrt{3}}•\frac{y}{x-\sqrt{3}}=-\frac{2}{3}$(x$≠±\sqrt{3}$),可求P的轨迹方程;
(2)设直线MN的方程为x=my+t,代入椭圆方程$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$,利用kOMkON=$\frac{2{t}^{2}-6}{3{t}^{2}-6{m}^{2}}$=-$\frac{2}{3}$,得2t2=2m2+3,即可证明结论.
解答 (1)解:由已知设点P的坐标为(x,y),由题意知$\frac{y}{x+\sqrt{3}}•\frac{y}{x-\sqrt{3}}=-\frac{2}{3}$(x$≠±\sqrt{3}$),
化简得P的轨迹方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$(x$≠±\sqrt{3}$)…(5分)
(2)证明:由题意M,N是椭圆C上非顶点的两点,且AP∥OM,BP∥ON,
则直线AP,BP斜率必存在且不为0,又由已知kAPkBP=-$\frac{2}{3}$.
因为AP∥OM,BP∥ON,所以kOMkON=-$\frac{2}{3}$…(6分)
设直线MN的方程为x=my+t,代入椭圆方程$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$,得(3+2m2)y2+4mty+2t2-6=0…①,…(7分)
设M,N的坐标分别为M(x1,y1),N(x2,y2),则y1+y2=-$\frac{4mt}{3+2{m}^{2}}$,y1y2=$\frac{2{t}^{2}-6}{3+2{m}^{2}}$…(8分)
所以kOMkON=$\frac{2{t}^{2}-6}{3{t}^{2}-6{m}^{2}}$=-$\frac{2}{3}$,得2t2=2m2+3…(10分)
又S△MON=$\frac{1}{2}$|t||y1-y2|=$\frac{2\sqrt{6}|t|\sqrt{{t}^{2}}}{4{t}^{2}}$=$\frac{\sqrt{6}}{2}$,
即△MON的面积为定值$\frac{\sqrt{6}}{2}$…(12分)
点评 本题考查轨迹方程,考查直线与椭圆的位置关系,考查斜率、面积的计算,属于中档题.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案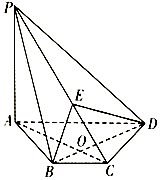 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.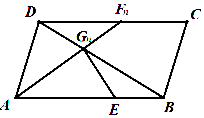 如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )
如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )