题目内容
16.椭圆$\frac{x^2}{m}+{y^2}=1$的离心率$e∈(\frac{1}{2},1)$,则m的取值范围是$m>\frac{4}{3}$或$0<m<\frac{3}{4}$.分析 当m>1时,a2=m.b2=1,c2=m-1,e2=$\frac{{c}^{2}}{{a}^{2}}=\frac{m-1}{m}∈(\frac{1}{4},1)$,
当0<m<1时,a2=1.b2=m,c2=1-m,e2=$\frac{1-m}{1}$∈($\frac{1}{4},1$).
解答 解:当m>1时,a2=m.b2=1,c2=m-1,e2=$\frac{{c}^{2}}{{a}^{2}}=\frac{m-1}{m}∈(\frac{1}{4},1)$,⇒m>$\frac{4}{3}$;
当0<m<1时,a2=1.b2=m,c2=1-m,e2=$\frac{1-m}{1}$∈($\frac{1}{4},1$)⇒0<m<$\frac{3}{4}$.
故答案为:0<m<$\frac{3}{4}$或m>$\frac{4}{3}$.
点评 本题考查了椭圆的方程中a2=b2+c2的关系,及离心率的计算,属于基础题.

练习册系列答案
相关题目
6.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,出行健步不为难,次日脚疼减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一人走了378里路,第一天健步行走,从第二天起因脚疼每天走的路程为前一天的一半,走了6天后到达目的地.”问此人最后一天走了( )
| A. | 6里 | B. | 12里 | C. | 24里 | D. | 36里 |
11.抛物线y2=20x的焦点到准线的距离是( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
1.下列语句是假命题的是( )
| A. | 正方形的四条边相等 | B. | 若x=0,则xy=0 | ||
| C. | $\sqrt{3}∈N$ | D. | 负数的平方是正数 |
8.如果方程Ax+By+C=0表示的直线是x轴,则A、B、C满足( )
| A. | A•C=0 | B. | B≠0 | C. | B≠0且A=C=0 | D. | A•C=0且B≠0 |
5.如图,正四面体ABCD的棱长为1,点E是棱CD的中点,则$\overrightarrow{AE}$•$\overrightarrow{AB}$=( )
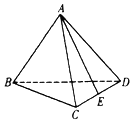

| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |