题目内容
已知如图,抛物线y2=2px(p>0)的焦点为F,A在抛物线上,其横坐标为4,且位于x轴上方,A到抛物线准线的距离等于5.过A作AB 垂直于y轴,垂足为B,OB的中点为M.
垂直于y轴,垂足为B,OB的中点为M.
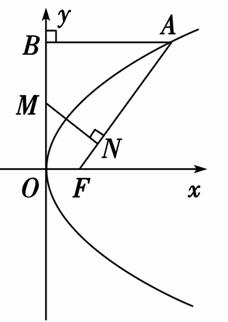
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标.
解析:(1)抛物线y2=2px(p>0)的准线为x=-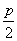 ,
,
于是4+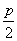 =5,所以p=2.
=5,所以p=2.
所以抛物线的标准方程为y2=4x.
(2)由(1)得点A的坐标是(4,4),
由题意得B(0,4),M(0,2),
因为F(1,0),所以kFA=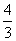 .
.
因为MN⊥FA,所以kMN=-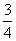 .
.
则FA所在直线的方程为y=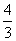 (x-1),
(x-1),
MN所在直线的方程为y-2=-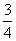 x.
x.
解方程组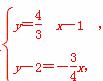 得
得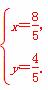
所以N .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则“
,则“ ”是“
”是“ ”成立的( )
”成立的( )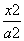 -
- =1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是____________.
=1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是____________.
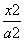 +
+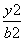 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为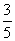 ,且点
,且点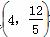 在椭圆上,则以椭圆的左、右焦点及短轴上的两个顶点为顶点的四边形的周长为
在椭圆上,则以椭圆的左、右焦点及短轴上的两个顶点为顶点的四边形的周长为 ( )
( )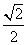 .
.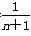 (n∈N*)与椭圆C在第一象限内相交于点An(xn,yn),记an=
(n∈N*)与椭圆C在第一象限内相交于点An(xn,yn),记an=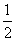 x
x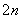 ,试证明:对∀n∈N*
,试证明:对∀n∈N* ,a1·a2·…·an>
,a1·a2·…·an>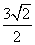 .设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
.设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.