题目内容
已知等轴双曲线C的中心在原点,焦点在x轴上,若等轴双曲线C与抛物线y2=16x的准线交于A,B两点,AB=4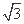 ,则等轴双曲线C的实轴长为 .
,则等轴双曲线C的实轴长为 .
4

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
题目内容
已知等轴双曲线C的中心在原点,焦点在x轴上,若等轴双曲线C与抛物线y2=16x的准线交于A,B两点,AB=4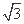 ,则等轴双曲线C的实轴长为 .
,则等轴双曲线C的实轴长为 .
4

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案