题目内容
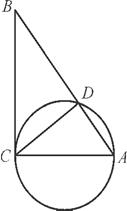
如图,AD是☉O的直径,AB是☉O的切线,M,N是圆上两点,直线MN交AD的延长线于点C,交☉O的切线于点B,且BM=MN=NC=1,求AB的长和☉O的半径.
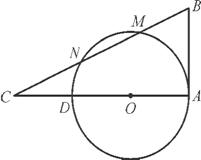
因为AD是☉O的直径,AB是☉O的切线,
直线BMN是☉O的割线,所以∠BAC=90°,
AB2=BM·BN.
因为BM=MN=NC=1,所以2BM2=AB2,
所以AB= .
.
因为AB2+AC2=BC2,所以2+AC2=9,AC=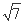 .
.
因为CN·CM=CD·CA,所以2=CD·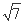 ,所以CD=
,所以CD=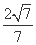 .所以☉O的半径为
.所以☉O的半径为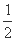 (CA-CD)=
(CA-CD)= .
.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于 .
A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于 .  AD.
AD.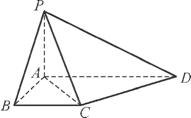
 对应的变换作用下得到的直线过点P(4,1),求实数k的值.
对应的变换作用下得到的直线过点P(4,1),求实数k的值.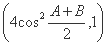 ,b=
,b= 1,2sin2
1,2sin2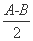 -3
-3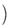 .
.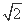 ,求角C的大小;
,求角C的大小;