题目内容
13.已知P,Q为动直线y=m(0<m<$\frac{{\sqrt{2}}}{2}$)与y=sinx和y=cosx在区间$[0,\frac{π}{2}]$上的左,右两个交点,P,Q在x轴上的投影分别为S,R.当矩形PQRS面积取得最大值时,点P的横坐标为x0,则( )| A. | ${x_0}<\frac{π}{8}$ | B. | ${x_0}=\frac{π}{8}$ | C. | $\frac{π}{8}<{x_0}<\frac{π}{6}$ | D. | ${x_0}>\frac{π}{6}$ |
分析 由题意知,P与Q关于直线$x=\frac{π}{4}$对称,设P(x,sinx),则矩形PQRS的面积为S(x)=($\frac{π}{2}$-2x)•sinx,(0<x<$\frac{π}{4}$),再利用导数求得矩形面积S(x)的最大值.
解答 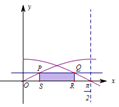 解:由题意知,P与Q关于直线$x=\frac{π}{4}$对称,设P(x,sinx),则$Q(\frac{π}{2}-x,sinx)$,∴$S(x)=(\frac{π}{2}-2x)sinx(0<x<\frac{π}{4})$,
解:由题意知,P与Q关于直线$x=\frac{π}{4}$对称,设P(x,sinx),则$Q(\frac{π}{2}-x,sinx)$,∴$S(x)=(\frac{π}{2}-2x)sinx(0<x<\frac{π}{4})$,
∴${S^'}(x)=-2sinx+(\frac{π}{2}-2x)cosx$,∴S″=-4cosx-($\frac{π}{2}$-2x)sinx,
∵$0<x<\frac{π}{4}$,∴S''(x)<0,∴S′(x)在区间$(0,\frac{π}{4})$上单调递减,
且${S^'}(0)=\frac{π}{2}>0$,${S^'}(\frac{π}{4})=-\sqrt{2}<0$,
∴S′(x)在区间$(0,\frac{π}{4})$存在唯一零点,即为x0.
令S′(x0)=0得:$2sin{x_0}=(\frac{π}{2}-2{x_0})cos{x_0}$,即$tan{x_0}=\frac{π}{4}-{x_0}$.
由不等式$tan{x_0}>{x_0}(0<{x_0}<\frac{π}{2})$得:$\frac{π}{4}-{x_0}>{x_0}$,解得:${x_0}<\frac{π}{8}$,
故选:A.
点评 考查三角函数的图象与性质、导数、零点、不等式等,考查数形结合思想、转化与化归思想,考查逻辑推理能力,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.已知$f(x)=\left\{\begin{array}{l}1+x,x∈R\\(1+i)x,x∉R\end{array}\right.$,则f[f(1-i)]等于( )
| A. | 3 | B. | 1 | C. | 2-i | D. | 3+i |
4.已知集合S={1,2},设S的真子集有m个,则m=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
1.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,双曲线 x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为8,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |
8.已知平面α⊥平面β,α∩β=l,直线m?α,直线n?β,且m⊥n,有以下四个结论:
①若n∥l,则m⊥β
②若m⊥β,则n∥l
③m⊥β和n⊥α同时成立
④m⊥β和n⊥α中至少有一个成立
其中正确的是( )
①若n∥l,则m⊥β
②若m⊥β,则n∥l
③m⊥β和n⊥α同时成立
④m⊥β和n⊥α中至少有一个成立
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
18.为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动,“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车…”铿锵有力的话语,传递了低碳生活、绿色出行的理念.某机构随机调查了本市500名成年市民某月的骑车次数,统计如下:
联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.记本市一个年满18岁的青年人月骑车的平均次数为μ.以样本估计总体.
(Ⅰ)估计μ的值;
(Ⅱ)在本市老年人或中年人中随机访问3位,其中月骑车次数超过μ的人数记为ξ,求ξ的分布列与数学期望.
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至30岁 | 6 | 14 | 20 | 32 | 40 | 48 |
| 31岁至44岁 | 4 | 6 | 20 | 28 | 40 | 42 |
| 45岁至59岁 | 22 | 18 | 33 | 37 | 19 | 11 |
| 60岁及以上 | 15 | 13 | 10 | 12 | 5 | 5 |
(Ⅰ)估计μ的值;
(Ⅱ)在本市老年人或中年人中随机访问3位,其中月骑车次数超过μ的人数记为ξ,求ξ的分布列与数学期望.
5.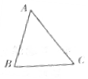 为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
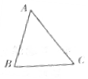 为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )| A. | (1+$\frac{\sqrt{3}}{2}$)米 | B. | 2米 | C. | (1+$\sqrt{3}$)米 | D. | (2+$\sqrt{3}$)米 |
5.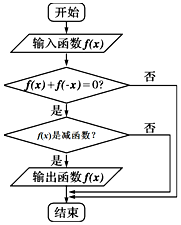 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |