题目内容
5．
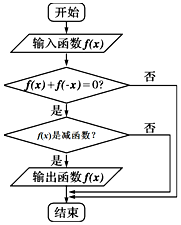执行如图所示的程序框图，若输入如下四个函数：①f（x）=sinx，②f（x）=cosx，③f（x）=$\frac{1}{x}$，④f（x）=lg$\frac{1-x}{1+x}$，则输出的函数是（ ）| A． | f（x）=sinx | B． | f（x）=cosx | C． | f（x）=$\frac{1}{x}$ | D． | f（x）=lg$\frac{1-x}{1+x}$ |
分析 由已知中的程序框图，可得该程序输出的函数即是奇函数，也是减函数，进而得到答案．
解答 解：由已知中的程序框图，可得该程序输出的函数即是奇函数，也是减函数，
A中，f（x）=sinx是奇函数，但在R上不是减函数，
B中，f（x）=cosx不是奇函数，在R上也不是减函数，
C中，f（x）=$\frac{1}{x}$是奇函数，但在R上不是减函数，
D中，f（x）=lg$\frac{1-x}{1+x}$是奇函数，且是定义域（-1，1）上的是减函数，
故选：C
点评 本题以程序框图为载体，考查了函数的单调性，函数的奇偶性，难度中档．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
13．已知P，Q为动直线y=m（0＜m＜$\frac{{\sqrt{2}}}{2}$）与y=sinx和y=cosx在区间$[0，\frac{π}{2}]$上的左，右两个交点，P，Q在x轴上的投影分别为S，R．当矩形PQRS面积取得最大值时，点P的横坐标为x0，则（ ）
| A． | ${x_0}＜\frac{π}{8}$ | B． | ${x_0}=\frac{π}{8}$ | C． | $\frac{π}{8}＜{x_0}＜\frac{π}{6}$ | D． | ${x_0}＞\frac{π}{6}$ |