题目内容
从-3、-2、-1、1、2、3中任取三个不同的数作为椭圆方程ax2+by2-c=0中的系数,则确定不同的椭圆的个数为 .
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出
>0,且
>0,由此推导出确定不同的椭圆的个数.
| c |
| a |
| c |
| b |
解答:
解:椭圆方程ax2+by2-c=0化为标准方程,得
+
=1,
∴
>0,且
>0,
∴从-3、-2、-1、1、2、3中任取三个不同的数作为椭圆方程ax2+by2-c=0中的系数,
则确定不同的椭圆的个数为
+
=12.
故答案为:12.
| x2 | ||
|
| y2 | ||
|
∴
| c |
| a |
| c |
| b |
∴从-3、-2、-1、1、2、3中任取三个不同的数作为椭圆方程ax2+by2-c=0中的系数,
则确定不同的椭圆的个数为
| A | 3 3 |
| A | 3 3 |
故答案为:12.
点评:本题考查椭圆的个数的求法,是基础题,解题时要认真审题,注意椭圆的性质的灵活运用.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
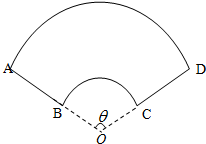 某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.
