题目内容
已知△ABC的面积为
，AC=2，∠BAC=60°，则BC= ．
| ||
| 2 |
考点：正弦定理
专题：计算题,解三角形
分析：先根据面积公式求出AB，再根据余弦定理求出BC的值即可．
解答：
解：根据面积公式△ABC的面积S=
AB•ACsin∠BAC=
=
×AB×2×
，
∴AB=1
又根据余弦定理BC2=AB2+AC2-2•AB•AC•cos∠BAC=1+4-2×1×2×
=3
∴BC=
，
故答案为：
．
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴AB=1
又根据余弦定理BC2=AB2+AC2-2•AB•AC•cos∠BAC=1+4-2×1×2×
| 1 |
| 2 |
∴BC=
| 3 |
故答案为：
| 3 |
点评：本题主要考察了余弦定理的应用，属于基本知识的考查．
练习册系列答案
相关题目
在△ABC中，角A，B，C所对的边分别为a，b，c，若a=1，b=
，A=30° 则角B等于（ ）
| 3 |
| A、60°或120° |
| B、30°或150° |
| C、60° |
| D、120° |
已知A={x|0≤x≤3}，B={y|0≤y≤3}，下列从集合A到集合B的对应关系不是映射的是（ ）
A、f：x→y=
| ||
B、f：x→y=
| ||
C、f：x→y=
| ||
D、f：x→y=
|
下列函数中，与函数y=x相同的函数是（ ）
A、y=
| ||||
B、y=(
| ||||
| C、y=lg10x | ||||
| D、y=2log2x |
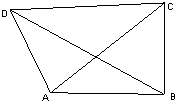如图：在平面四边形ABCD中，AB=3
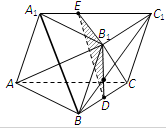如图，在三棱柱ABC-A1B1C1中，D是BC的中点．