题目内容
已知sin2x+cos2x=1,函数y=cos2x+2sinx+3且x∈[
,
],求函数值域.
| π |
| 6 |
| 2π |
| 3 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值,三角函数的图像与性质
分析:函数解析式利用同角三角函数间的基本关系变形,再利用二次函数的性质即可求出值域.
解答:
解:y=cos2x+2sinx+3=-sin2x+2sinx+4=-(sinx-1)2+5,
∵x∈[
,
],
∴sinx∈[
,1],
当sinx=1时,ymax=5;
当sinx=
时,ymin=4
,
则函数的值域为[4
,5].
∵x∈[
| π |
| 6 |
| 2π |
| 3 |
∴sinx∈[
| 1 |
| 2 |
当sinx=1时,ymax=5;
当sinx=
| 1 |
| 2 |
| 3 |
| 4 |
则函数的值域为[4
| 3 |
| 4 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
圆心是O(-3,4),半径长为5的圆的方程是( )
| A、(x-3)2+(y+4)2=5 |
| B、(x-3)2+(y+4)2=25 |
| C、(x+3)2+(y-4)2=5 |
| D、(x+3)2+(y-4)2=25 |
在△ABC中a、b、c分别是角A、B、C的对边,
=
,角A=( )
| tanA |
| tanB |
| ||
| b |
| A、30° | B、45° |
| C、60° | D、90° |
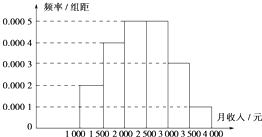 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):