题目内容
(本小题满分13分)如图,在三棱柱ABC—A1B1C1中,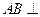 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,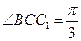 ,E为CC1的中点。
,E为CC1的中点。
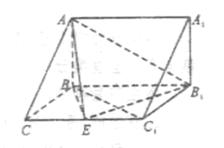
(1)求证: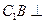 平面ABC;
平面ABC;
(2)求二面角A—B1E—B的大小。
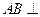 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,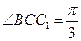 ,E为CC1的中点。
,E为CC1的中点。
(1)求证:
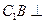 平面ABC;
平面ABC;(2)求二面角A—B1E—B的大小。
解:(1)因为AB⊥侧面 ,
, 侧面
侧面 ,故AB⊥BCl,
,故AB⊥BCl,
在△BCCl中,BC=1, ,
, ,
,
可得△BCE为等边三角形, ,所以BC⊥BCl.
,所以BC⊥BCl.
而BC AB=B,∴C1B⊥平面AB C.…………………………6分
AB=B,∴C1B⊥平面AB C.…………………………6分
(2)在△ 中,
中, ,
, ,
,
 ,
,
∴
 BE⊥EBl.
BE⊥EBl.
又∵AB⊥侧面BBlC1C,∴AB⊥BlE,
又AB BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
∴∠AEB即是二面角 的平面角.
的平面角.
在Rt△ABE中, ,故
,故 .
.
所以二面角 的大小为
的大小为 .……………12分(亦可建立空间直角坐标系求解)
.……………12分(亦可建立空间直角坐标系求解)
 ,
, 侧面
侧面 ,故AB⊥BCl,
,故AB⊥BCl,在△BCCl中,BC=1,
 ,
, ,
,可得△BCE为等边三角形,
 ,所以BC⊥BCl.
,所以BC⊥BCl.而BC
 AB=B,∴C1B⊥平面AB C.…………………………6分
AB=B,∴C1B⊥平面AB C.…………………………6分(2)在△
 中,
中, ,
, ,
,
 ,
,∴

 BE⊥EBl.
BE⊥EBl.又∵AB⊥侧面BBlC1C,∴AB⊥BlE,
又AB
 BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,∴∠AEB即是二面角
 的平面角.
的平面角.在Rt△ABE中,
 ,故
,故 .
.所以二面角
 的大小为
的大小为 .……………12分(亦可建立空间直角坐标系求解)
.……………12分(亦可建立空间直角坐标系求解)略

练习册系列答案
相关题目
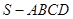 中,
中,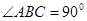 ,
,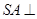 面
面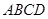 ,
, ,
,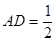 。
。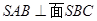 ;
;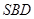 的距离。
的距离。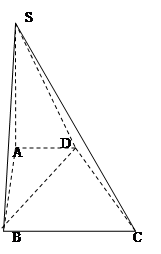
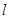 上有无数点不在平面
上有无数点不在平面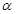 内,则
内,则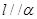

 中,已知
中,已知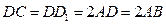 ,
,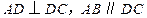 .
.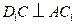 ;
;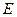 是
是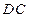 上一点,试确定
上一点,试确定 平面
平面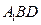 ,并证明.
,并证明.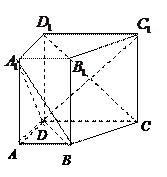
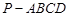 中,底面
中,底面 是直角梯形,
是直角梯形,
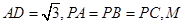 是线段
是线段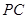 上不同于
上不同于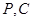 的任意一点,且
的任意一点,且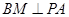

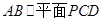 ;
;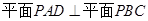 ;
;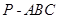 的体积。
的体积。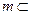 平面
平面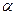 ,则“平面
,则“平面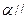 平面
平面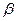 ”是“
”是“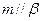 ”的
”的
 形
形 是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成
是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成 一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体
一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体 对
对