题目内容

18．已知等比数列{an}中，a1a2a3=8．
（1）求a2；
（2）若公比q＞1，且a1+2a2+3a3=17，求前7项的和S7．

分析 （1）由题意和等比数列的性质可得a23=8，解方程可得；
（2）结合（1）可得q的方程，解得q，进而可得首项，代入求和公式可得．

解答 解：（1）∵等比数列{an}中a1a2a3=8，
∴a23=8，解得a2=2；
（2）∵a1+2a2+3a3=17，∴$\frac{2}{q}$+4+6q=17，
整理可得6q2-13q+2=0，解得q=2或q=$\frac{1}{6}$，
∵公比q＞1，∴q=2，∴a1=$\frac{2}{q}$=1，
∴前7项的和S7=$\frac{1×（1-{2}^{7}）}{1-2}$=127

点评 本题考查等比数列的通项公式和求和公式，属基础题．

练习册系列答案
相关题目
8．过点A（1，2），且平行于向量$\overrightarrow{n}$=（2，1）的直线方程为（　　）
A．x-2y-3=0B．x-2y+3=0C．2x-y+3=0D．以上都不正确
9．（1）已知sin（π+α）=$\frac{1}{3}$，求sin（-3π+α）的值．
（2）已知cos（$\frac{π}{3}+α$）=-$\frac{1}{2}$，求cos（$α-\frac{5π}{3}$）的值．
6．已知函数f（x）=kx-2，f（1）=-1，则f（2）=（　　）
A．0B．-1C．1D．2
13．对于向量的集合A叫A={$\overrightarrow{v}$=（x，y）|x2+y2≤1}中的任意两个向量$\overrightarrow{{v}_{1}}$、$\overrightarrow{{v}_{2}}$与两个非负实数α、β；求证：向量α$\overrightarrow{{v}_{1}}$+β$\overrightarrow{{v}_{2}}$的大小不超过α+β．
3．定义在R上的函数f（x）满足f（x+3）=-f（x），且当x∈[-6，0）时，f（x）=$\sqrt{1-x}$，则f（2017）=$\sqrt{6}$．
10．若“?x∈R，x2+mx+2m-3≥0”为假命题，则m的取值范围是{m|m＞2，或m＜6}．
7．已知sinα＜0且tanα＞0，则角α所在的象限是（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
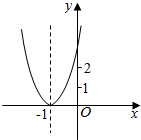13．已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（-1，0），下列结论：①abc＜0；②b2-4ac=0；③a＞2；④4a-2b+c＞0．其中正确结论的个数是（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网