题目内容
18.已知函数f(x)=x2+m与函数$g(x)=-ln\frac{1}{x}-3x$$(x∈[\frac{1}{2},2])$的图象上至少存在一对关于x轴对称的点,则实数m的取值范围是( )| A. | $[\frac{5}{4}+ln2,2]$ | B. | $[2-ln2,\frac{5}{4}+ln2]$ | C. | $[\frac{5}{4}+ln2,2+ln2]$ | D. | [2-ln2,2] |
分析 由已知,得到方程m=-lnx+3x-x2在[$\frac{1}{2}$,2]上有解,构造函数f(x)=-lnx+3x-x2,求出它的值域,得到m的范围即可.
解答 解:由已知,得到方程x2+m=ln$\frac{1}{x}$+3x?m=-lnx+3x-x2在[$\frac{1}{2}$,2]上有解.
设f(x)=-lnx+3x-x2,
求导得:f′(x)=-$\frac{1}{x}$+3-2x=-$\frac{2{x}^{2}-3x+1}{x}$=-$\frac{(2x-1)(x-1)}{x}$,
∵$\frac{1}{2}$≤x≤2,
令f′(x)=0,解得x=$\frac{1}{2}$或x=1,
当f′(x)>0时,$\frac{1}{2}$<x<1函数单调递增,
当f′(x)<0时,1<x<2函数单调减,
∴在x=1有唯一的极值点,
∵f($\frac{1}{2}$)=ln2+$\frac{5}{4}$,f(2)=-ln2+2,f(x)极大值=f(1)=2,且知f(2)<f($\frac{1}{2}$),
故方程m=-lnx+3x-x2在[$\frac{1}{2}$,2]上有解等价于2-ln2≤m≤2.
从而m的取值范围为[2-ln2,2].
故选:D.
点评 本题考查了构造函数法求方程的解及参数范围;关键是将已知转化为方程x2+m=ln$\frac{1}{x}$+3x?m=-lnx+3x-x2在上有解.

练习册系列答案
相关题目
8.若i为虚数单位,则复数$\frac{1+i}{3-i}$等于( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{4}+\frac{1}{2}i$ | C. | $\frac{2}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
9.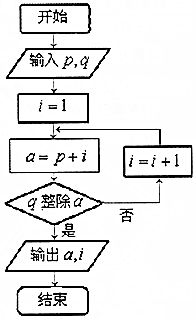 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )| A. | a=3,i=1 | B. | a=18,i=16 | C. | a=18,i=15 | D. | a=9,i=7 |
6.设等差数列{an}的前n项和为Sn,若S9=54,则a2+a4+a9=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 36 |
7.设p:x2-x<1,$q:{log_2}({x^2}-x)<0$,则非p是非q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |