题目内容
13. 若y=f(x)的图象如图所示,定义F(x)=$\int_0^x{f(t)dt$,x∈[0,1],则下列对F(x)的性质描述正确的有(1)(2)(4).(把所有正确的序号都填上)
若y=f(x)的图象如图所示,定义F(x)=$\int_0^x{f(t)dt$,x∈[0,1],则下列对F(x)的性质描述正确的有(1)(2)(4).(把所有正确的序号都填上)(1)F(x)是[0,1]上的增函数;
(2)F′(1)=0;
(3)F(x)是[0,1]上的减函数;
(4)?x0∈[0,1]使得F(1)=f(x0).
分析 求F′(x)=f(x)根据函数图象可判断(1)(2)正确,(3)不正确,由拉格朗日中值定理值(4)正确.
解答 解:由F′(x)=f(x)x∈[0,1],由图象可知F′(x)>0,
∴F(x)是[0,1]上的增函数,(1)对,(3)不对;
F′(x)=f(x)则F′(1)=f(1)=0,
故(2)对;
由拉格朗日中值定理可知,?x0∈[0,1]使得F(1)=f(x0).
故(4)对,
故答案为(1)(2)(4)
点评 主要考察导数的几何意义,属于基础题.

练习册系列答案
相关题目
8.已知集合A={x|x2-1≤0},B={x|lnx<0},则A∪B=( )
| A. | {x|x≤1} | B. | {x|0<x<1} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
18.在平面直角坐标系中,一束光线从点M(-2,3)出发,被直线y=x-1反射后到达点N(1,6),则这束光线从M到N所经过的路程为( )
| A. | 10$\sqrt{3}$ | B. | 3$\sqrt{10}$ | C. | 2$\sqrt{10}$ | D. | 3$\sqrt{2}$ |
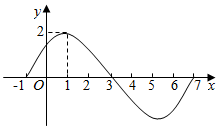 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).