题目内容
16.在如图所示的茎叶图中,甲、乙两组数据的中位数分别是( )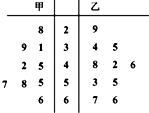
| A. | 45和47 | B. | 45 和44 | C. | 45和42 | D. | 45和45 |
分析 根据茎叶图,分析出各组数据,结合中位数的定义,可得答案.
解答 解:由已知可得:
甲组数据共9个数,从小到大分别为:
28,31,39,42,45,55,57,58,66,
其中位数为45;
乙组数据共10个数,从小到大分别为:
29,34,35,42,46,48,53,55,66,67,
其中位数为$\frac{1}{2}$(46+48)=47;
故选:A.
点评 本题考查的知识点是茎叶图,中位数的计算,难度不大,属于基础题.

练习册系列答案
相关题目
7.已知e=2.71828…,设函数f(x)=$\frac{1}{2}$x2-bx+alnx存在极大值点x0,且对于b的任意可能取值,恒有极大值f(x0)<0,则下列结论中正确的是( )
| A. | 存在x0=$\sqrt{a}$,使得f(x0)<-$\frac{1}{e}$ | B. | 存在x0=$\sqrt{a}$,使得f(x0)>-e | ||
| C. | a的最大值为e3 | D. | 0<a<e3 |
8.已知函数f(x)=$\frac{2}{x+1}$,点O为坐标原点,点An(n,f(n))(n∈N*),向量$\overrightarrow j=(0,1)$,θn是向量$\overrightarrow{O{A_n}}$与$\overrightarrow j$的夹角,则$\frac{{cos{θ_1}}}{{sin{θ_1}}}+\frac{{cos{θ_2}}}{{sin{θ_2}}}+\frac{{cos{θ_1}}}{{sin{θ_1}}}+…+\frac{{cos{θ_{2016}}}}{{sin{θ_{2016}}}}$=( )
| A. | $\frac{2015}{1008}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{4032}{2017}$ |