��Ŀ����
8����֪����f��x��=$\frac{2}{x+1}$����OΪ����ԭ�㣬��An��n��f��n������n��N*��������$\overrightarrow j=��0��1��$����n������$\overrightarrow{O{A_n}}$��$\overrightarrow j$�ļнǣ���$\frac{{cos{��_1}}}{{sin{��_1}}}+\frac{{cos{��_2}}}{{sin{��_2}}}+\frac{{cos{��_1}}}{{sin{��_1}}}+��+\frac{{cos{��_{2016}}}}{{sin{��_{2016}}}}$=��������| A�� | $\frac{2015}{1008}$ | B�� | $\frac{2017}{2016}$ | C�� | $\frac{2016}{2017}$ | D�� | $\frac{4032}{2017}$ |
���� ���$\overrightarrow{O{A}_{n}}$������ƽ����������������ʽ����cos��n������ͬ�����Ǻ����Ĺ�ϵ�ó�sin��n�������$\frac{cos{��}_{n}}{sin{��}_{n}}$=$\frac{2}{n��n+1��}$��Ȼ��ʹ�������ͼ��ɣ�
��� �⣺$\overrightarrow{O{A}_{n}}$=��n��$\frac{2}{n+1}$����
��cos��n=$\frac{\overrightarrow{O{A}_{n}}•\overrightarrow{i}}{|\overrightarrow{O{A}_{n}}||\overrightarrow{i}|}$=$\frac{\frac{2}{n+1}}{\sqrt{{n}^{2}+\frac{4}{��n+1��^{2}}}}$=$\frac{2}{\sqrt{��n+1��^{2}{n}^{2}+4}}$��
��sin��n=$\sqrt{1-co{s}^{2}{��}_{n}}$=$\frac{n��n+1��}{\sqrt{��n+1��^{2}{n}^{2}+4}}$��
��$\frac{cos{��}_{n}}{sin{��}_{n}}$=$\frac{2}{n��n+1��}$=2��$\frac{1}{n}-\frac{1}{n+1}$����
��$\frac{{cos{��_1}}}{{sin{��_1}}}+\frac{{cos{��_2}}}{{sin{��_2}}}+\frac{{cos{��_1}}}{{sin{��_1}}}+��+\frac{{cos{��_{2016}}}}{{sin{��_{2016}}}}$=2��1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+��+$\frac{1}{2016}-\frac{1}{2017}$��
=2��1-$\frac{1}{2017}$��=$\frac{4032}{2017}$��
��ѡD��
���� ���⿼����ƽ�����������������㣬������ͣ�����ͨ���ǹؼ��������е��⣮

| A�� | 1-i | B�� | 1+i | C�� | 2-2i | D�� | 2+2i |
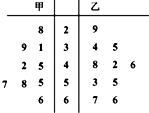
| A�� | 45��47 | B�� | 45 ��44 | C�� | 45��42 | D�� | 45��45 |
| A�� | x-y-1=0 | B�� | x+y-1=0 | C�� | x-y+1=0 | D�� | x+y+1=0 |
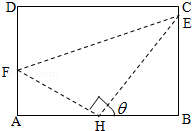 ��ͼ������ABCD���ڽ�Rt��FHE����H��ֱ�Ƕ��㣩��H��AB���е㣬E��F�ֱ������߶�BC��AD�ϣ���֪AB=2��AD=$\sqrt{3}$���ǡ�BHE=�ȣ�
��ͼ������ABCD���ڽ�Rt��FHE����H��ֱ�Ƕ��㣩��H��AB���е㣬E��F�ֱ������߶�BC��AD�ϣ���֪AB=2��AD=$\sqrt{3}$���ǡ�BHE=�ȣ�