题目内容
4.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P,Q可以重合),则B1P+PQ的最小值为$\frac{3}{2}$.分析 将△AB1C1绕边AC1旋转到AMC1位置,使得平面AMC1和平面ACC1在同一平面内,则M到平面ABCD的距离即为B1P+PQ的最小值,利用勾股定理解出即可.
解答 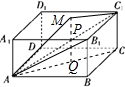 解:将△AB1C1绕边AC1旋转到AMC1位置,使得平面AMC1和平面ACC1在同一平面内,
解:将△AB1C1绕边AC1旋转到AMC1位置,使得平面AMC1和平面ACC1在同一平面内,
过点M作MQ⊥平面ABCD,交AC1于P,垂足为Q,则MQ为B1P+PQ的最小值.
∵AB=$\sqrt{2}$,BC=AA1=1,
∴AC1=$\sqrt{2+1+1}$=2,AM=AB1=$\sqrt{3}$,
∵sin∠C1AC=$\frac{C{C}_{1}}{A{C}_{1}}$=$\frac{1}{2}$,
∴∠C1AC=30°,
∴∠MAQ=2∠C1AC=60°,
∴MQ=AM•sin∠MAQ=$\sqrt{3}×\frac{\sqrt{3}}{2}=\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查了空间距离的计算,将两线段转化为同一平面上是解决最小值问题的一般思路,属于中档题.

练习册系列答案
相关题目
13.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的渐近线方程为( )
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
12.已知函数y=f(x)=x2+1,则在x=2,△x=0.1时,△y的值为( )
| A. | 0.40 | B. | 0.41 | C. | 0.43 | D. | 0.44 |
16.在如图所示的茎叶图中,甲、乙两组数据的中位数分别是( )
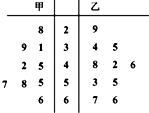

| A. | 45和47 | B. | 45 和44 | C. | 45和42 | D. | 45和45 |
14.下列函数既是奇函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x3 | C. | y=log2x | D. | y=-3-x |