题目内容
已知动圆M与定圆x2+(y-
)2=
相外切,且与定直线y=-
相切,动圆圆心M的轨迹记为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设直线y=kx+m与曲线C相交于A,B两点,Q(x0,y0)是曲线C上异于A、B的点,曲线C在A,B处的切线相交于P点,曲线C在点Q处的切线l与直线PA,PB分别交于点D、E,求△QAB与△PDE的面积之比.
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
(Ⅰ)求曲线C的方程;
(Ⅱ)设直线y=kx+m与曲线C相交于A,B两点,Q(x0,y0)是曲线C上异于A、B的点,曲线C在A,B处的切线相交于P点,曲线C在点Q处的切线l与直线PA,PB分别交于点D、E,求△QAB与△PDE的面积之比.
考点:直线与圆锥曲线的综合问题,直线和圆的方程的应用
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设F(0,
),M到定直线y=-
的距离为d,动圆M的半径为R,由已知得:|MF|=R+
,由抛物线的定义得C的方程为x2=2y.
(Ⅱ)设A(x1,y1),B(x2,y2),记△QAB、△PDE的面积分别为S1、S2,由
,得x2-2kx-2m=0,由此利用韦达定理、根的判别式、弦长公式、点到直线的距离公式能求出△QAB与△PDE的面积之比.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅱ)设A(x1,y1),B(x2,y2),记△QAB、△PDE的面积分别为S1、S2,由
|
解答:
解:(Ⅰ)设F(0,
),M到定直线y=-
的距离为d,动圆M的半径为R,
由已知得:|MF|=R+
,d=R,即|MF|与M到定直线y=-
的距离相等,
由抛物线的定义得C的方程为x2=2y.(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),记△QAB、△PDE的面积分别为S1、S2,
由
,得x2-2kx-2m=0,则x1+x2=2k,x1x2=-2m,
△=4k2+8m>0,(7分)
|AB|=
•
,Q到AB的距离d1=
,
则S1=
|AB|•d1=
|kx0+m-y0|,(8分)
由x2=2y,得y=
,y′=x,
则曲线C在A处的切线y-y1=x1(x-x1),即y=x1x-
x12,①
同理曲线C在B处的切线为y=x2x-
x22,②
由①②得P(
,
),即P(k,-m),(10分)
同理曲线C在Q处的切线为y=x0x-
x02,
D(
,
),E(
,
),(11分)
则|DE|=
=
=
,
P到DE的距离d2=
=
,
则S2=
|DE|d2=
|kx0-y0+m|,(14分)
所以
=2,
故△QAB与△PDE的面积之比为2.(15分)
| 1 |
| 2 |
| 1 |
| 4 |
由已知得:|MF|=R+
| 1 |
| 4 |
| 1 |
| 2 |
由抛物线的定义得C的方程为x2=2y.(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),记△QAB、△PDE的面积分别为S1、S2,
由
|
△=4k2+8m>0,(7分)
|AB|=
| 1+k2 |
| 4k2+8m |
| |kx0+m-y0| | ||
|
则S1=
| 1 |
| 2 |
| k2+2m |
由x2=2y,得y=
| x2 |
| 2 |
则曲线C在A处的切线y-y1=x1(x-x1),即y=x1x-
| 1 |
| 2 |
同理曲线C在B处的切线为y=x2x-
| 1 |
| 2 |
由①②得P(
| x1+x2 |
| 2 |
| x1x2 |
| 2 |
同理曲线C在Q处的切线为y=x0x-
| 1 |
| 2 |
D(
| x1+x0 |
| 2 |
| x1x0 |
| 2 |
| x2+x0 |
| 2 |
| x2x0 |
| 2 |
则|DE|=
(
|
=
| ||
| 2 |
| (x1+x2)-4x1x2 |
=
| 1+x02 |
| k2+2m |
P到DE的距离d2=
|
| ||||||
|
=
| |kx0-y0+m| | ||
|
则S2=
| 1 |
| 2 |
| 1 |
| 2 |
| k2+2m |
所以
| S1 |
| S2 |
故△QAB与△PDE的面积之比为2.(15分)
点评:本题主要考查抛物线的几何性质、直线与抛物线、圆等知识,同时考查解析几何的基本思想方法和运算求解能力.

练习册系列答案
相关题目
在如图所示的程序框图中输入n=3,结果会输出( )


| A、2 | B、4 | C、6 | D、8 |
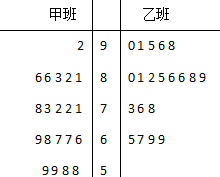 我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.
我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.