Question

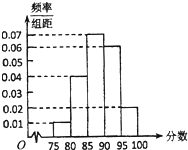某次有1000人参加数学摸底考试，其成绩的频率分布直方图如图所示，规定85分及以上为优秀．
（1）下表是这次考试成绩的频数分布表，求正整数a，b的值；

区间	[75，80）	[80，85）	[85，90）	[90，95）	[95，100]
人数	50	a	350	300	b

（2）现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析，求其中成绩为优秀的学生人数．

Answer 1

考点：分层抽样方法

专题：概率与统计

分析：（1）由题意可得：a=0.04×5×1000，b=0.02×5×1000．
（2）设其中成绩为优秀的学生人数为x，则

x

40

=

350+300+100

1000

，解得x即可．

解答： 解：（1）由题意可得：a=0.04×5×1000=200，b=0.02×5×1000=100．
（2）设其中成绩为优秀的学生人数为x，则

x

40

=

350+300+100

1000

，解得x=30．
因此其中成绩为优秀的学生人数为30．

点评：本题考查了频率分布直方图的有关计算、分层抽样的定义及其计算，考查了推理能力，属于基础题．