题目内容
若点P(x,y)在曲线
(θ为参数,θ∈R)上,则
的取值范围是 .
|
| y |
| x |
考点:参数方程化成普通方程,直线与圆的位置关系
专题:坐标系和参数方程
分析:由
(θ为参数,θ∈R)可得:k=
=
.因此k可以看作P(2,0)与圆:x2+y2=1上的点的连线的直线的斜率的取值范围.利用点到直线的距离公式即可得出.
|
| y |
| x |
| sinθ |
| cosθ-2 |
解答:
解:由
(θ为参数,θ∈R)可得:k=
因此k可以看作P(2,0)与圆:x2+y2=1上的点的连线的直线的斜率的取值范围.
设过点P的直线方程为:y=k(x-2),化为kx-y-2k=0,
∵
≤1,解得k2≤
.
解得-
≤k≤
.
∴
的取值范围是[-
,
].
故答案为:[-
,
].
|
| y |
| x |
因此k可以看作P(2,0)与圆:x2+y2=1上的点的连线的直线的斜率的取值范围.
设过点P的直线方程为:y=k(x-2),化为kx-y-2k=0,
∵
| |-2k| | ||
|
| 1 |
| 3 |
解得-
| ||
| 3 |
| ||
| 3 |
∴
| y |
| x |
| ||
| 3 |
| ||
| 3 |
故答案为:[-
| ||
| 3 |
| ||
| 3 |
点评:本题考查了圆的参数方程、斜率计算公式、直线与圆的位置关系,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
 如图已知P、Q是棱长为a的正方体ABCD-A1B1C1D1的面AA1D1D和A1B1C1D1的中心.
如图已知P、Q是棱长为a的正方体ABCD-A1B1C1D1的面AA1D1D和A1B1C1D1的中心.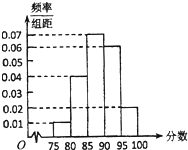 某次有1000人参加数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及以上为优秀.
某次有1000人参加数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及以上为优秀.