题目内容
 如图,直角梯形ABCD中,AB∥CD,AB=
如图,直角梯形ABCD中,AB∥CD,AB=| 1 |
| 2 |
| 1 |
| 4 |
(1)证明:EF⊥AD;
(2)证明:MN∥平面ADE;
(3)若AB=1,BC=2,求几何体ABCDE的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)先证明出EF⊥BC,进而根据面面垂直的性质判断出EF⊥平面ABCD,最后根据线面垂直的性质证明出EF⊥AD.
(2)取AE中点G,连接MG,DG,先证明出四边形DGMN是平行四边形,推断出DG∥MN,进而根据线面平行的判定定理证明出MN∥平面ADE.
(3)利用梯形面积公式求得底面面积,进而在三角形△BCE中求得EF,最后求得体积.
(2)取AE中点G,连接MG,DG,先证明出四边形DGMN是平行四边形,推断出DG∥MN,进而根据线面平行的判定定理证明出MN∥平面ADE.
(3)利用梯形面积公式求得底面面积,进而在三角形△BCE中求得EF,最后求得体积.
解答:
(1)证明:∵△BCE为等边三角形,F是BC的中点,
∴EF⊥BC,
又∵平面ABCD⊥平面BCE,交线为BC,EF?平面BCE
∴EF⊥平面ABCD;
又∵AD?平面ABCD,
∴EF⊥AD.
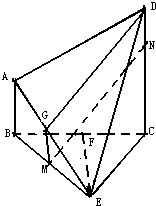
(2)证明:取AE中点G,连接MG,DG,
∵AG=GE,BM=ME,
∴GM∥AB,且GM=
AB,
∵AB∥CD,AB=
CD,DN=
DC,
∴DN∥AB,且DN=
AB,
∴四边形DGMN是平行四边形,
∴DG∥MN,
又∵DG?平面ADE,MN?平面ADE,
∴MN∥平面ADE
(3)依题,直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=2,BC=2
则直角梯形ABCD的面积为S梯形ABCD=
(AB+CD)×BC=
(1+2)×2=3,
由(1)可知EF⊥平面ABCD,即EF是四棱锥E-ABCD的高
在等边△BCE中,由边长BC=2,得EF=2×sin600=
,
故几何体ABCDE的体积为V E-ABCD=
•S梯形ABCD•EF=
×3×
=
.
∴EF⊥BC,
又∵平面ABCD⊥平面BCE,交线为BC,EF?平面BCE
∴EF⊥平面ABCD;
又∵AD?平面ABCD,
∴EF⊥AD.

(2)证明:取AE中点G,连接MG,DG,
∵AG=GE,BM=ME,
∴GM∥AB,且GM=
| 1 |
| 2 |
∵AB∥CD,AB=
| 1 |
| 2 |
| 1 |
| 4 |
∴DN∥AB,且DN=
| 1 |
| 2 |
∴四边形DGMN是平行四边形,
∴DG∥MN,
又∵DG?平面ADE,MN?平面ADE,
∴MN∥平面ADE
(3)依题,直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=2,BC=2
则直角梯形ABCD的面积为S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
由(1)可知EF⊥平面ABCD,即EF是四棱锥E-ABCD的高
在等边△BCE中,由边长BC=2,得EF=2×sin600=
| 3 |
故几何体ABCDE的体积为V E-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了线面垂直和线面平行的判定定理的应用.考查了学生分析能力和空间观察能力.

练习册系列答案
相关题目
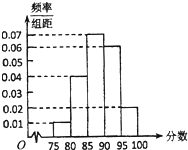 某次有1000人参加数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及以上为优秀.
某次有1000人参加数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及以上为优秀.