题目内容
若y=|x-3|+|x+a|的最小值是5，求a．
考点：函数的最值及其几何意义
专题：不等式的解法及应用
分析：根据绝对值不等式的性质即可得到结论．
解答：
解：y=|x-3|+|x+a|=|3-x|+|x+a|≥|3-x+x+a|=|3+a|，
故最小值为|3+a|=5，
解得a=2或a=-8．
故最小值为|3+a|=5，
解得a=2或a=-8．
点评：本题主要考查不等式的应用，要求熟练掌握绝对值不等式的求解方法．
练习册系列答案
相关题目
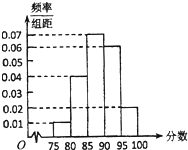某次有1000人参加数学摸底考试，其成绩的频率分布直方图如图所示，规定85分及以上为优秀．