题目内容
给出下列命题:
①若ab>0,a>b,则
<
;
②若已知直线x=m与函数f(x)=sinx,g(x)=sin(
-x)的图象分别交于点M,N,则|MN|的最大值为
;
③若数列an=n2+λn(λ∈N*)为单调递增数列,则λ取值范围是λ<-2;
④若直线l的斜率k<1,则直线l的倾斜角-
<α<
;
其中真命题的序号是: .
①若ab>0,a>b,则
| 1 |
| a |
| 1 |
| b |
②若已知直线x=m与函数f(x)=sinx,g(x)=sin(
| π |
| 2 |
| 2 |
③若数列an=n2+λn(λ∈N*)为单调递增数列,则λ取值范围是λ<-2;
④若直线l的斜率k<1,则直线l的倾斜角-
| π |
| 2 |
| π |
| 4 |
其中真命题的序号是:
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用不等式的性质即可得出;
②利用和差化积和正弦函数的单调性即可得出;
③利用二次函数的单调性即可得出;
④利用直线的斜率与倾斜角的关系即可得出.
②利用和差化积和正弦函数的单调性即可得出;
③利用二次函数的单调性即可得出;
④利用直线的斜率与倾斜角的关系即可得出.
解答:
解:①.∵ab>0,a>b,∴
>
,即
<
,因此正确;
②.|MN|=|sinx-sin(
-x)|=|sinx-cosx|=
|sin(x-
)|≤
,故②正确;
③.若数列an=n2+λn(λ∈N*)为单调递增数列,则-
<0,即λ>0,因此不正确;
④若直线l的斜率k<1,则直线l的倾斜角0<k<
或
<k<π,因此不正确.
综上可知:只有①②正确.
故答案为:①②.
| a |
| ab |
| b |
| ab |
| 1 |
| a |
| 1 |
| b |
②.|MN|=|sinx-sin(
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
③.若数列an=n2+λn(λ∈N*)为单调递增数列,则-
| λ |
| 2 |
④若直线l的斜率k<1,则直线l的倾斜角0<k<
| π |
| 4 |
| π |
| 2 |
综上可知:只有①②正确.
故答案为:①②.
点评:本题综合考查了不等式的性质、和差化积和正弦函数的单调性、二次函数的单调性、直线的斜率与倾斜角的关系、正切函数的单调性等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知
=(-1,t),
=(2,2),若∠ABO=90°,则t=( )
| OA |
| OB |
| A、2 | B、4 | C、5 | D、8 |
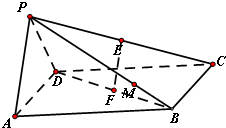 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.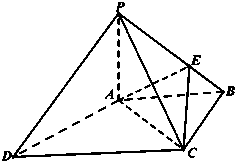 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
 四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为
四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为