题目内容
下列命题中正确的是( )
A、若
| ||||||||||||
B、向量
| ||||||||||||
| C、空间任意两个向量共面 | ||||||||||||
D、若
|
考点:共线向量与共面向量,平行向量与共线向量
专题:平面向量及应用,空间向量及应用
分析:A.若
∥
,
∥
,则
与
所在直线平行或重合;
B.向量
、
、
共面,则它们所在直线可能共面,也可能不共面;
C.根据共面向量基本定理即可判断出;
D.利用向量共线定理可知:若
∥
,则存在唯一的实数λ,使使
=λ
或
=λ
.
| a |
| b |
| b |
| c |
| a |
| c |
B.向量
| a |
| b |
| c |
C.根据共面向量基本定理即可判断出;
D.利用向量共线定理可知:若
| a |
| b |
| a |
| b |
| b |
| a |
解答:
解:A.若
∥
,
∥
,则
与
所在直线平行或重合,因此不正确;
B.向量
、
、
共面,则它们所在直线可能共面,也可能不共面,因此不正确;
C.根据共面向量基本定理可知:空间任意两个向量共面,正确;
D.若
∥
,则存在唯一的实数λ,使使
=λ
或
=λ
,因此不正确.
综上可知:只有C正确.
故选:C.
| a |
| b |
| b |
| c |
| a |
| c |
B.向量
| a |
| b |
| c |
C.根据共面向量基本定理可知:空间任意两个向量共面,正确;
D.若
| a |
| b |
| a |
| b |
| b |
| a |
综上可知:只有C正确.
故选:C.
点评:本题考查了共线向量基本定理、共面向量基本定理、向量平行与直线平行的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a>1,b>1,且lnalnb=
,则ab( )
| 1 |
| 4 |
| A、有最大值1 |
| B、有最小值1 |
| C、有最大值e |
| D、有最小值e |
在一次学习方法交流会上,需要交流示范学校的5篇论文和非示范学校的3篇论文,交流顺序可以是任意的,则最先和最后交流的论文不能来自同类学校的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
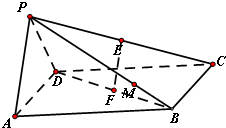 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.