题目内容
已知圆C的圆心是直线x-y+1=0与y轴的交点,且圆C与直线x+y+3=0相切,则圆的标准方程为 .
考点:圆的标准方程
专题:直线与圆
分析:对于直线x-y+1=0,令x=0求出y的值,确定出圆心C坐标,利用点到直线的距离公式求出圆C的半径,写出圆的标准方程即可.
解答:
解:对于直线x-y+1=0,令x=0,得到y=1,即圆心C(0,1),
∵圆C与直线x+y+3=0相切,
∴圆心C到直线的距离d=r,即r=d=
=2
,
则圆C的标准方程为x2+(y-1)2=8.
故答案为:x2+(y-1)2=8
∵圆C与直线x+y+3=0相切,
∴圆心C到直线的距离d=r,即r=d=
| |1+3| | ||
|
| 2 |
则圆C的标准方程为x2+(y-1)2=8.
故答案为:x2+(y-1)2=8
点评:此题考查了圆的标准方程,涉及的知识有:直线与坐标轴的交点,点到直线的距离公式,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线y-1=k(x-3)被圆(x-2)2+(y-2)2=4所截得的最短弦长等于( )
A、
| ||
B、2
| ||
C、2
| ||
D、
|
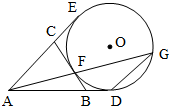 如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是
如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是在一次学习方法交流会上,需要交流示范学校的5篇论文和非示范学校的3篇论文,交流顺序可以是任意的,则最先和最后交流的论文不能来自同类学校的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
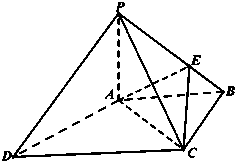 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点. 四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为
四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1,则点B到平面PAC的距离为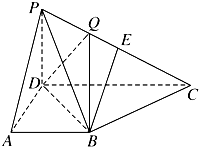 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为