题目内容
8.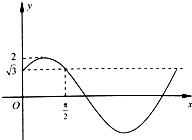 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<|φ|<π)在一个周期内的图象如图所示.(1)求函数f(x)的解析式;
(2)求f(x)在[0,π]上的单调区间.
分析 (1)根据图形,直接代入点(0,$\sqrt{3}$),($\frac{π}{2}$,$\sqrt{3}$)列出方程即可;
(2)求出函数解析式后,直接代入y=sinx的单调增或减区间,解出x的取值范围即可.
解答 解:(1)由图形易知A=2,
将点(0,$\sqrt{3}$),($\frac{π}{2}$,$\sqrt{3}$)代入,有$\left\{\begin{array}{l}{sinφ=\frac{\sqrt{3}}{2}}\\{sin(\frac{π}{2}ω+φ)=\frac{\sqrt{3}}{2}}\end{array}\right.$
∵0<|φ|<π,∴$\left\{\begin{array}{l}{φ=\frac{π}{3}}\\{ω=\frac{2}{3}}\end{array}\right.$,故f(x)=2sin($\frac{2}{3}x$+$\frac{π}{3}$).
(2)由(1)知f(x)=2sin($\frac{2}{3}x$+$\frac{π}{3}$),
要使f(x)单调递增,则2k$π-\frac{π}{2}$≤$\frac{2}{3}x+\frac{π}{3}$≤$2kπ+\frac{π}{2}$,
即$3kπ-\frac{5π}{4}$≤x≤3kπ+$\frac{π}{4}$,k∈Z,f(x)的单调递增区间为[$3kπ-\frac{5π}{4}$,kπ+$\frac{π}{4}$],k∈Z.
k=0,得[-$\frac{5π}{4}$,$\frac{π}{4}$],∴f(x)在[0,π]上的单调递增区间[0,$\frac{π}{4}$].
要f(x)单调递减,则$2kπ+\frac{π}{2}$≤$\frac{2}{3}x+\frac{π}{3}$≤$2kπ+\frac{3π}{2}$,
即$3kπ+\frac{π}{4}≤$ x $≤\$ 3k$π+\frac{7π}{4}$,k∈Z,∴f(x)的单调递减区间为[3kπ+$\frac{π}{4}$,3k$π+\frac{7π}{4}$],k∈Z.
取k=0,得[$\frac{π}{4}$,$\frac{7π}{4}$],∴f(x)在[0,π]上的单调递减区间[$\frac{π}{4}$,π].
故f(x)在[0,π]上的单调递增区间[0,$\frac{π}{4}$],单调递减区间为[$\frac{π}{4}$,π].
点评 本题主要考查了三角函数图形求解析式,以及三角函数的单调增减区间,属中等题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案| A. | 2${\;}^{\frac{1}{2}}$<($\frac{1}{2}$)3 | B. | ($\frac{3}{4}$)${\;}^{-\frac{1}{2}}$>($\frac{3}{4}$)${\;}^{-\frac{1}{3}}$ | ||
| C. | 53.1<33.1 | D. | 0.3${\;}^{-\frac{1}{5}}$>0.3${\;}^{-\frac{1}{3}}$ |
| A. | $-\frac{1}{3}$ | B. | $-\frac{2}{3}$ | C. | -1 | D. | $-\frac{4}{3}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | ${2^{-\frac{3}{2}}}$ |
| A. | 2x-y+5=0或2x-y-5=0 | B. | 2x+y+5=0或2x+y-5=0 | ||
| C. | $2x-y+\sqrt{5}=0$或$2x+y-\sqrt{5}=0$ | D. | $2x-y+\sqrt{5}=0$或$2x-y-\sqrt{5}=0$ |
| A. | y=x2+4x+4(x≥-2) | B. | y=x2-4x+4(x≥0) | C. | y=x2+2(x≥0) | D. | y=x2-2(x≥0) |
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |