题目内容
9.等比数列{an}满足:a1=a(a>0),${a_1}+1{,^{\;}}{a_2}+2{,^{\;}}{a_3}+3$成等比数列,若{an}唯一,则a的值等于$\frac{1}{3}$.分析 设公比为q,由条件得:aq2-4aq+3a-1=0关于q∈R且q≠0有唯一解,由此能求出结果.
解答 解:设公比为q,
∵等比数列{an}满足:a1=a(a>0),${a_1}+1{,^{\;}}{a_2}+2{,^{\;}}{a_3}+3$成等比数列,
∴(aq+2)2=(a+1)(aq2+3),
整理,得:aq2-4aq+3a-1=0,
∵{an}唯一,∴由条件得:aq2-4aq+3a-1=0关于q∈R且q≠0有唯一解,
注意到a>0,△=16a2-4a(3a-1)>0恒成立,
∴3a-1=0,$a=\frac{1}{3}$(q=0为方程的增解).
故答案为:$\frac{1}{3}$.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}{3x+3(x≤-1)}\\{f(x-1)+1(x>-1)}\end{array}\right.$方程f(x)=x+1的解从小到大排成一个数列{an},该数列的前n项的和为Sn,则$\frac{2{S}_{n+3}+10}{n}$的最小值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
20.把函数$f(x)=\sqrt{2}sin(2x-\frac{π}{4})$的图象上每个点的横坐标扩大到原来的4倍,再向左平移$\frac{π}{3}$,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
17.已知$a={(\sqrt{2})^{\frac{4}{3}}}$,$b={2^{\frac{2}{5}}}$,$c={9^{\frac{1}{3}}}$,则( )
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
4.已知集合A={x||x|≤2,x∈Z},$B=\left\{{x|\frac{1}{x+1}≤0,x∈R}\right\}$,则A∩∁RB=( )
| A. | (-1,2] | B. | [-1,2] | C. | {-1,0,1,2} | D. | {0,1,2} |
14.双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$的充要条件是( )
| A. | m>1 | B. | $m>\frac{1}{2}$ | C. | m>2 | D. | m≥1 |
18.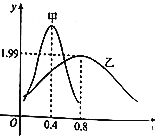 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |