题目内容
已知函数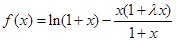 .
.
(Ⅰ)若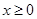 时,
时,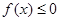 ,求
,求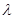 的最小值;
的最小值;
(Ⅱ)设数列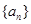 的通项
的通项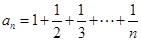 ,证明:
,证明: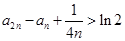 .
.
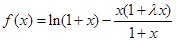 .
.(Ⅰ)若
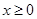 时,
时,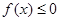 ,求
,求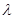 的最小值;
的最小值;(Ⅱ)设数列
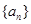 的通项
的通项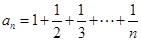 ,证明:
,证明: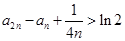 .
.(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
 (Ⅱ)见解析
(Ⅱ)见解析(Ⅰ)由已知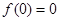 ,
, ,
,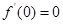 .
.
若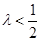 ,则当
,则当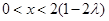 时,
时, ,所以
,所以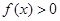 .
.
若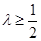 ,则当
,则当 时,
时,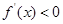 ,所以当
,所以当 时,
时,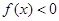 .
.
综上,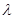 的最小值是
的最小值是 .
.
(Ⅱ)证明:令 .由(Ⅰ)知,当
.由(Ⅰ)知,当 时,
时,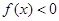 ,
,
即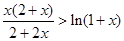 .
.
取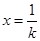 ,则
,则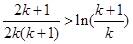 .
.
于是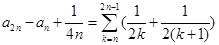
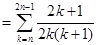


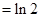 .
.
所以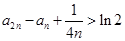 .
.
(1)通过求导的方法研究函数的单调性,进而判断满足条件的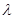 的范围,确定其最小值;(2)借助第一问的结论,得到不等式
的范围,确定其最小值;(2)借助第一问的结论,得到不等式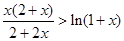 进而构造
进而构造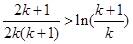 达到证明不等式的目的.
达到证明不等式的目的.
【考点定位】本题考查导数的应用与不等式的证明,考查学生的分类讨论思想和利用构造法证明不等式的解题能力.
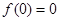 ,
, ,
,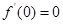 .
.若
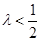 ,则当
,则当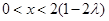 时,
时, ,所以
,所以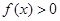 .
.若
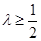 ,则当
,则当 时,
时,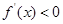 ,所以当
,所以当 时,
时,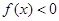 .
.综上,
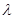 的最小值是
的最小值是 .
.(Ⅱ)证明:令
 .由(Ⅰ)知,当
.由(Ⅰ)知,当 时,
时,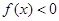 ,
,即
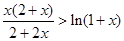 .
.取
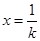 ,则
,则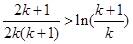 .
.于是
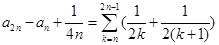
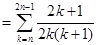


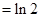 .
.所以
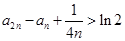 .
.(1)通过求导的方法研究函数的单调性,进而判断满足条件的
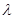 的范围,确定其最小值;(2)借助第一问的结论,得到不等式
的范围,确定其最小值;(2)借助第一问的结论,得到不等式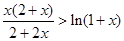 进而构造
进而构造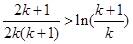 达到证明不等式的目的.
达到证明不等式的目的.【考点定位】本题考查导数的应用与不等式的证明,考查学生的分类讨论思想和利用构造法证明不等式的解题能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
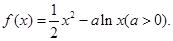
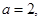 求
求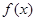 在
在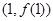 处的切线方程;
处的切线方程;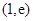 上恰有两个零点,求
上恰有两个零点,求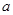 的取值范围.
的取值范围.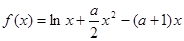 (
(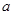 为常数)
为常数) 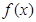 的单调区间;
的单调区间;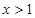 时,
时,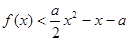 ,求
,求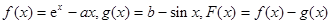 .
.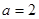 时,对任意
时,对任意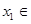 R,存在
R,存在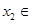 R,使
R,使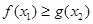 ,求实数
,求实数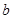 的取值范围;
的取值范围;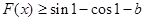 对任意
对任意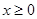 恒成立,求实数
恒成立,求实数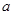 的取值范围.
的取值范围.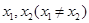 是函数
是函数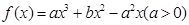 的两个极值点.
的两个极值点.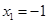 ,
,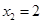 ,求函数
,求函数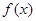 的解析式;
的解析式;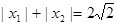 ,求实数
,求实数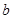 的最大值;
的最大值;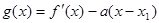 ,若
,若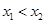 ,且
,且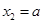 ,求函数
,求函数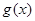 在
在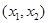 内的最小值.(用
内的最小值.(用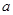 表示)
表示)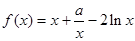 ,
,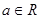
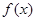 的单调区间;
的单调区间;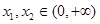 ,且
,且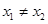 ,有
,有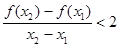 ,求实数
,求实数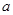 的取值范围.
的取值范围.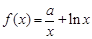 ,
,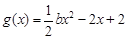 ,
,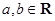
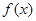 的单调区间;
的单调区间;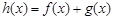 ,当
,当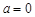 时,
时,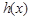 在
在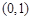 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数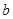 的取值范围;
的取值范围;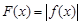 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线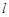 与
与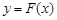 的图象有两个切点
的图象有两个切点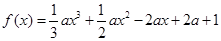 的图象经过四个象限的一个充分必要条件是( )
的图象经过四个象限的一个充分必要条件是( )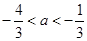
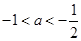
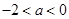 ?
?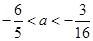
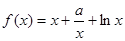 ,
,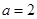 时,求函数
时,求函数 的单调增区间;
的单调增区间;