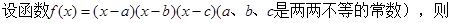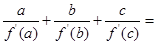题目内容
若函数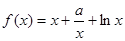 ,
,
(Ⅰ)当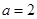 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(Ⅱ)函数 是否存在极值.
是否存在极值.
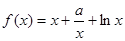 ,
,(Ⅰ)当
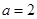 时,求函数
时,求函数 的单调增区间;
的单调增区间;(Ⅱ)函数
 是否存在极值.
是否存在极值.(1)函数 的单调增区间为
的单调增区间为
(2)当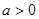 时,函数
时,函数 存在极值;当
存在极值;当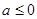 时,函数
时,函数 不存在极值
不存在极值
 的单调增区间为
的单调增区间为
(2)当
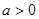 时,函数
时,函数 存在极值;当
存在极值;当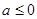 时,函数
时,函数 不存在极值
不存在极值试题分析:解:(1)由题意,函数
 的定义域为
的定义域为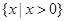 2分
2分当
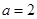 时,
时,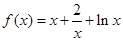 ,
, 3分
3分令
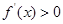 ,即
,即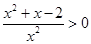 ,得
,得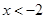 或
或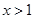 5分
5分又因为
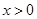 ,所以,函数
,所以,函数 的单调增区间为
的单调增区间为 6分
6分(2)
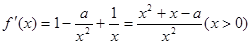 7分
7分解法一:令
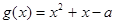 ,因为
,因为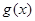 对称轴
对称轴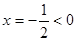 ,所以只需考虑
,所以只需考虑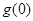 的正负,
的正负,当
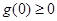 即
即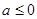 时,在(0,+∞)上
时,在(0,+∞)上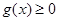 ,
,即
 在(0,+∞)单调递增,
在(0,+∞)单调递增, 无极值 10分
无极值 10分当
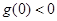 即
即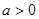 时,
时,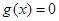 在(0,+∞)有解,所以函数
在(0,+∞)有解,所以函数 存在极值.…12分
存在极值.…12分综上所述:当
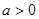 时,函数
时,函数 存在极值;当
存在极值;当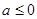 时,函数
时,函数 不存在极值.…14分
不存在极值.…14分解法二:令
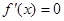 即
即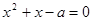 ,记
,记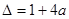
当
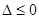 即
即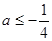 时,
时,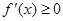 ,
, 在(0,+∞)单调递增,无极值 9分
在(0,+∞)单调递增,无极值 9分当
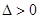 即
即 时,解
时,解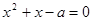 得:
得: 或
或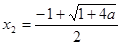
若
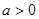 则
则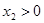 ,列表如下:
,列表如下: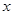 | (0,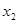 ) ) | 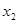 | (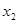 ,+∞) ,+∞) |
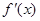 | — | 0 | + |
 | ↘ | 极小值 | ↗ |
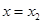 时函数
时函数 取到极小值,即
取到极小值,即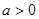 函数
函数 存在极小值。 11分
存在极小值。 11分若
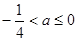 ,则
,则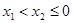 ,
, 在(0,+∞)单调递减,不存在极值。 13分
在(0,+∞)单调递减,不存在极值。 13分综上所述,当
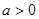 时,函数
时,函数 存在极值,当
存在极值,当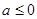 时。函数
时。函数 不存在极值 14分
不存在极值 14分点评:主要是考查了导数在研究函数中的运用,判定函数单调性以及函数极值,属于基础题。

练习册系列答案
相关题目
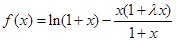 .
.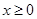 时,
时,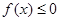 ,求
,求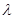 的最小值;
的最小值;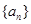 的通项
的通项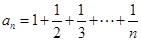 ,证明:
,证明: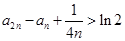 .
.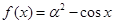 ,则
,则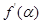 等于( )
等于( ) 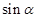
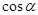
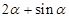
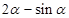
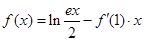 ,
,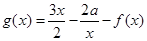 (其中
(其中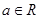 ).
).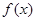 的单调区间;
的单调区间;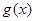 在区间
在区间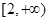 上为增函数,求
上为增函数,求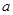 的取值范围;
的取值范围;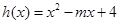 ,当
,当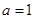 时,若存在
时,若存在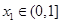 ,对任意的
,对任意的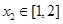 ,总有
,总有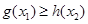 成立,求实数
成立,求实数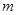 的取值范围.
的取值范围.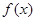 的定义域是
的定义域是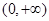 ,
,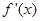 是
是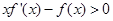 在
在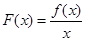 的单调区间;
的单调区间;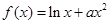 ,求
,求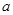 的取值范围;
的取值范围;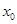 是
是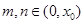 ,求证:
,求证: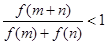
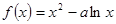 在(1,2)上是增函数,
在(1,2)上是增函数,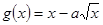 在(0,1)上是减函数。
在(0,1)上是减函数。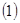 求
求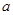 的值;
的值;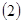 当
当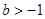 时,若
时,若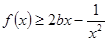 在
在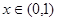 内恒成立,求实数
内恒成立,求实数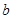 的取值范围;
的取值范围;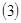 求证:方程
求证:方程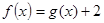 在
在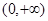 内有唯一解.
内有唯一解.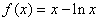 ,
,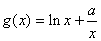 ,(
,(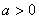 ).
).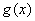 的极值;
的极值;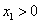 ,函数
,函数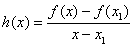 ,
, 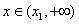 ,判断并证明
,判断并证明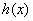 的单调性;
的单调性;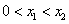 ,试比较
,试比较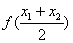 与
与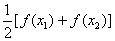 ,并加以证明.
,并加以证明.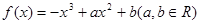
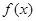 在区间(0,1)上单调递增,试求a的取值范围;
在区间(0,1)上单调递增,试求a的取值范围;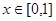 时,
时,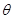 ,试求当
,试求当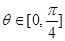 时,a的取值范围.
时,a的取值范围.