题目内容
已知函数 ,
, ,
,
⑴求函数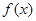 的单调区间;
的单调区间;
⑵记函数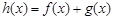 ,当
,当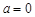 时,
时,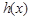 在
在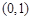 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数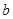 的取值范围;
的取值范围;
⑶记函数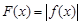 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线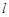 与
与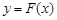 的图象有两个切点
的图象有两个切点
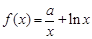 ,
,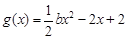 ,
,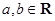
⑴求函数
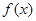 的单调区间;
的单调区间;⑵记函数
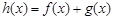 ,当
,当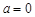 时,
时,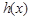 在
在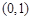 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数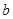 的取值范围;
的取值范围;⑶记函数
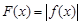 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线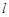 与
与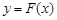 的图象有两个切点
的图象有两个切点(1)当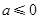 时,
时, 为单调增区间,当
为单调增区间,当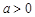 时,
时, 为单调减区间,
为单调减区间, 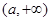 为单调增区间.
为单调增区间.
(2)
(3)在第二问的基础上,根据函数的单调性以及导数的几何意义来证明。
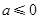 时,
时, 为单调增区间,当
为单调增区间,当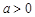 时,
时, 为单调减区间,
为单调减区间, 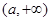 为单调增区间.
为单调增区间.(2)

(3)在第二问的基础上,根据函数的单调性以及导数的几何意义来证明。
试题分析:(1)因为
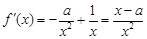 ,
, ①若
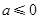 ,则
,则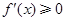 ,
,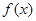 在
在 上为增函数,2分 ②若
上为增函数,2分 ②若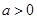 ,令
,令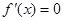 ,得
,得 ,
,当
 时,
时, ;当
;当 时,
时,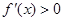 .
.所以
 为单调减区间,
为单调减区间,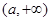 为单调增区间. 综上可得,当
为单调增区间. 综上可得,当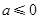 时,
时, 为单调增区间,
为单调增区间,当
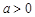 时,
时, 为单调减区间,
为单调减区间, 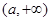 为单调增区间. 4分
为单调增区间. 4分(2)
 时,
时,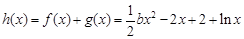 ,
, , 5分
, 5分 在
在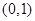 上有且只有一个极值点,即
上有且只有一个极值点,即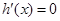 在
在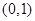 上有且只有一个根且不为重根,
上有且只有一个根且不为重根,由
 得
得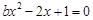 ,
, (i)
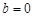 ,
, ,满足题意;…… 6分
,满足题意;…… 6分(ii)
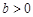 时,
时,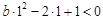 ,即
,即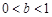 ;… 7分
;… 7分(iii)
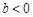 时,
时,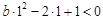 ,得
,得 ,故
,故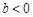 ; 综上得:
; 综上得: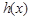 在
在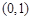 上有且只有一个极值点时,
上有且只有一个极值点时, . ………8分注:本题也可分离变量求得.
. ………8分注:本题也可分离变量求得.(3)证明:由(1)可知:
(i)若
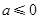 ,则
,则 ,
,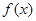 在
在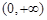 上为单调增函数,
上为单调增函数,所以直线
 与
与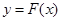 的图象不可能有两个切点,不合题意. 9分
的图象不可能有两个切点,不合题意. 9分(ⅱ)若
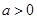 ,
,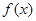 在
在 处取得极值
处取得极值 .
.若
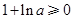 ,
,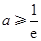 时,由图象知不可能有两个切点.10分
时,由图象知不可能有两个切点.10分故
 ,设
,设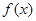 图象与
图象与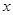 轴的两个交点的横坐标为
轴的两个交点的横坐标为 (不妨设
(不妨设 ),
),则直线
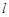 与
与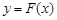 的图象有两个切点即为直线
的图象有两个切点即为直线 与
与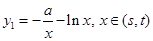 和
和 的切点.
的切点. ,
, ,
,设切点分别为
 ,则
,则 ,且
,且 ,
,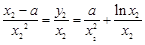 ,
,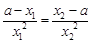 ,
, 即
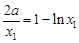 ① ,
① , 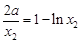 ② ,
② ,  ③ ,
③ ,①-②得:
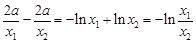 ,
, 由③中的
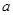 代入上式可得:
代入上式可得: ,即
,即 ,12分
,12分令
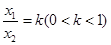 ,则
,则 ,令
,令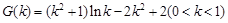 ,因为
,因为 ,
,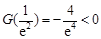 ,故存在
,故存在 ,使得
,使得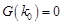 ,
,即存在一条过原点的直线
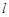 与
与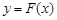 的图象有两个切点.14分
的图象有两个切点.14分点评:主要是考查了导数在研究函数中的运用,属于难度题。

练习册系列答案
相关题目
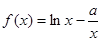 (
(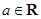 ).
).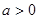 时,判断
时,判断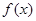 在定义域上的单调性;
在定义域上的单调性;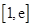 上的最小值为
上的最小值为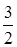 ,求
,求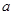 的值;
的值;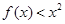 在
在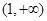 上恒成立,试求
上恒成立,试求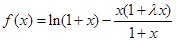 .
.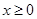 时,
时,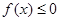 ,求
,求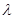 的最小值;
的最小值;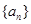 的通项
的通项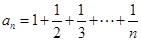 ,证明:
,证明: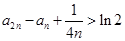 .
.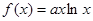 图像上点
图像上点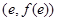 处的切线与直线
处的切线与直线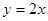 平行(其中
平行(其中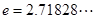 ),
),
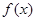 的解析式;
的解析式;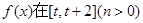 上的最小值;
上的最小值;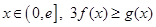 恒成立,求实数
恒成立,求实数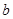 的取值范围。
的取值范围。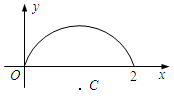
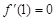 ;②
;②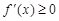 ;③
;③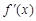 为减函数;④若
为减函数;④若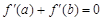 ,则a+b=2.
,则a+b=2.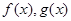 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当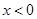 时,
时,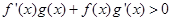 ,且g(-3)=0,则不等式
,且g(-3)=0,则不等式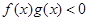 的解集是 ( )
的解集是 ( )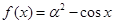 ,则
,则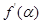 等于( )
等于( ) 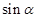
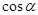
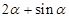
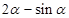
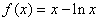 ,
,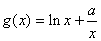 ,(
,(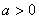 ).
).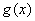 的极值;
的极值;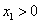 ,函数
,函数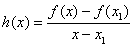 ,
, 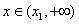 ,判断并证明
,判断并证明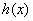 的单调性;
的单调性;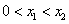 ,试比较
,试比较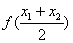 与
与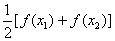 ,并加以证明.
,并加以证明.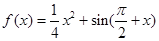 ,
,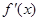 为
为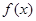 的导函数,则
的导函数,则