题目内容
“x≠2或y≠1”是“x+y≠3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:根据逆否命题的等价性,只需要判断x+y=3与x=1且y=2的条件关系即可.
若x=0,y=3时,满足x+y=3,但此时x=1且y=2,不成立,即充分性不成立.
若x=1,y=2时,则x+y=3成立,即必要性成立.
即x+y=3是x=1且y=2的必要不充分条件,
即“x≠1或y≠2”是“x+y≠3”的必要不充分条件,
故选:B
若x=0,y=3时,满足x+y=3,但此时x=1且y=2,不成立,即充分性不成立.
若x=1,y=2时,则x+y=3成立,即必要性成立.
即x+y=3是x=1且y=2的必要不充分条件,
即“x≠1或y≠2”是“x+y≠3”的必要不充分条件,
故选:B
点评:本题主要考查充分条件和必要条件的应用,利用逆否命题的等价性将条件转化为容易判断的条件关系是解决本题的关键.

练习册系列答案
相关题目
下列各选项中,正确的是( )
| A、若p∨q为真命题,则p∧q为真命题 | ||||||||||||||||
| B、命题“若x<-1,则x2-2x-3>0”的否命题为“若x<-1,则x2-2x-3≤0” | ||||||||||||||||
| C、已知命题p:?x∈R使x2+x-1<0,则?p为:?x∈R使得x2+x-1≥0 | ||||||||||||||||
D、设
|
若角α的终边在直线y=2x上,则sinα等于( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
观察如图:

若第n行的各数之和等于20112,则n=( )

若第n行的各数之和等于20112,则n=( )
| A、2011 | B、2012 |
| C、1006 | D、1005 |
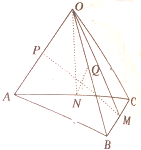 如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.
如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.