题目内容
在球面积26πcm2的球内作一内接圆柱,它的底面半径和高的比为1:3,求圆柱的全面积.
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:得出球的半径为
,底面半径为r,高为
,运用R2=r2+(
)2,求解r,运用面积公式得出答案.
| ||
| 2 |
| 3r |
| 2 |
| 3r |
| 2 |
解答:
解:∵球面积26πcm2,
∴球的半径为
,
∵球内作一内接圆柱,它的底面半径和高的比为1:3,
∴R2=r2+(
)2,
r=
,l=h=3
,
∴S底=2π×(
)2=4π,
S侧=2πrl=2π×
×3
=12π,
∴圆柱的全面积为16π.
∴球的半径为
| ||
| 2 |
∵球内作一内接圆柱,它的底面半径和高的比为1:3,
∴R2=r2+(
| 3r |
| 2 |
r=
| 2 |
| 2 |
∴S底=2π×(
| 2 |
S侧=2πrl=2π×
| 2 |
| 2 |
∴圆柱的全面积为16π.
点评:本题综合考查了球与圆柱的组合体,确定半径,高,母线之间的关系,运用面积公式求解即可,难度不大,属于中档题,计算准确.

练习册系列答案
相关题目
“x-1≠0”是“(x-1)(x-2)≠0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分也非必要条件 |
过点(0,4)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
“x≠2或y≠1”是“x+y≠3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
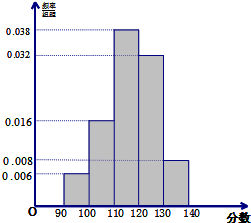 某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.