题目内容
12.函数y=x2-2x-3,x∈R的单调减区间为(-∞,1].分析 抛物线解析式配方后找出对称轴,根据a大于0,得到抛物线开口向上,利用二次函数单调性判断即可.
解答 解:函数y=x2-2x-3=x2-2x+1-4=(x-1)2-4,
∵a=1,对称轴为直线x=1,
∴抛物线开口向上,
则函数y=x2-2x-3,x∈R的单调减区间为(-∞,1],
故答案为:(-∞,1]
点评 此题考查了函数的单调性及其单调区间,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
2.复数z=1-i,则$\overrightarrow{z}$对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.下列叙述中正确的是( )
| A. | “m=2”是“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行”的充分条件 | |
| B. | “方程Ax2+By2=1表示椭圆”的充要条件是“A≠B” | |
| C. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02≥0” | |
| D. | 命题“a、b都是偶数,则a+b是偶数”的逆否命题为“a+b不是偶数,则a、b都是奇数” |
2.已知z1=m+i,z2=1-2i,若$\frac{{z}_{1}}{{z}_{2}}$为实数,则实数m的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |

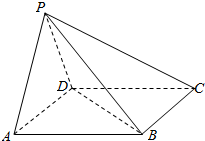 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD