题目内容
17．如图是一个空间几何体的三视图，则该几何体的表面积为64+4π．
分析 几何体为长方体挖去一个半球，把三视图中的数据代入公式计算即可．
解答 解：由三视图可知该几何体为长方体挖去一个半球得到的，长方体的棱长分别为4，4，2，半球的半径为2．
∴S=4×4+4×2×4+4×4-π×22+$\frac{1}{2}×4π×{2}^{2}$=64+4π．
故答案为64+4π．
点评 本题考查了空间几何体的三视图和面积计算，属于基础题．
练习册系列答案
相关题目
12．下列是函数y=x3-2x2-x+2 的零点的是（ ）
| A． | 1 | B． | 0 | C． | 3 | D． | 8 |
2．复数z=1-i，则$\overrightarrow{z}$对应的点所在的象限为（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
9．已知集合A={x|-1＜x＜4}，B={x|-2＜x＜3}，则A∩B=（ ）
| A． | {x|-1＜x＜3} | B． | {x|0≤x≤2} | C． | {0，1，2} | D． | {0，1，2，3} |
6．定义代数运算a?b=$\sqrt{1-\frac{1}{2}ab}$-ka-2，则当方程x?x=0有两个不同解时，实数k的取值范围是（ ）
| A． | $（-\sqrt{2}，-\frac{{\sqrt{6}}}{2}）∪（\frac{{\sqrt{6}}}{2}，\sqrt{2}）$ | B． | $[-\sqrt{2}，-\frac{{\sqrt{6}}}{2}）∪（\frac{{\sqrt{6}}}{2}，\sqrt{2}]$ | C． | $[-\sqrt{2}，-\frac{{\sqrt{6}}}{2}]∪[\frac{{\sqrt{6}}}{2}，\sqrt{2}]$ | D． | $[\frac{{\sqrt{6}}}{2}，\sqrt{2}]$ |
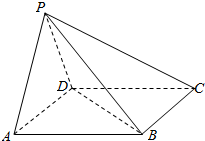如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAD是等腰三角形∠APD=90°，且平面PAD⊥平面ABCD