题目内容
方程x2-2ax-b2+16=0（a，b∈R），若a∈[0，6]，b∈[0，4]，则方程没有实根的概率为 ．
考点：几何概型
专题：概率与统计
分析：作出不等式组对应的平面区域，利用几何概型的概率公式求出相应的面积即可得到结论．
解答：
解：若关于x的一元二次方程x2-2（a-2）x-b2+16=0，
则△=4（a-2）2-4（16-b2）＜0，
即（a-2）2+b2＜16，
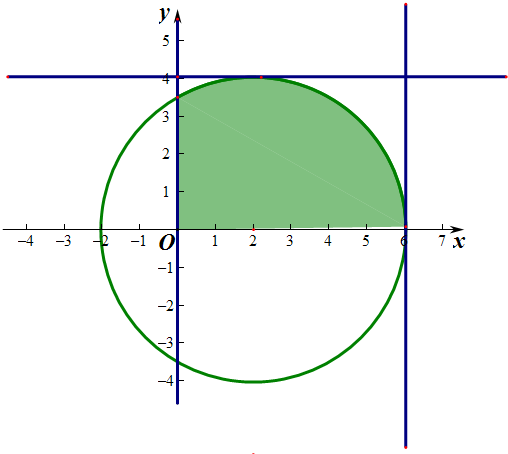
作出不等式组对应的平面区域如图：
则阴影部分的面积S=
π•42+
×2×4sin60°=
π+2
则由几何概型的概率公式可得方程x2-2（a-2）x-b2+16=0没有实根概率P=
=
..
解：若关于x的一元二次方程x2-2（a-2）x-b2+16=0，则△=4（a-2）2-4（16-b2）＜0，
即（a-2）2+b2＜16，
作出不等式组对应的平面区域如图：
则阴影部分的面积S=
| 2 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
| 3 |
则由几何概型的概率公式可得方程x2-2（a-2）x-b2+16=0没有实根概率P=
| ||||
| 4×6 |
3
| ||
| 36 |
点评：本题主要考查概率的计算，根据几何概型的概率公式是解决本题的关键，注意利用数形结合进行求解．．
练习册系列答案
相关题目
已知变量x，y的值如表所示；如果y与x线性相关且回归直线方程为y=bx+
，则实数b=（ ）
| 7 |
| 2 |
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某品牌香水瓶的三视图如图（单位：cm），则该几何体的表面积为（ ）
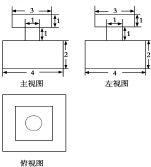
A、（95-
| ||
B、（94-
| ||
C、（94+
| ||
D、（95+
|
曲线C的方程为
+
=1，其中m，n是将一枚骰子先后投掷两次所得点数，事件A=“方程
+
=1表示焦点在x轴上的椭圆”，那么P（A）=（ ）
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示，在河岸 ac一侧测量河的宽度，测量以下四组数据，较适宜的是（ ）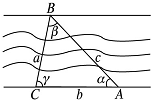 
| A、c，α，γ |
| B、c，b，α |
| C、c，a，β |
| D、b，α，γ |