题目内容
 将等腰直角三角板ADC与一个角为30°的直角三角板ABC拼在一起组成如图所示的平面四边形
将等腰直角三角板ADC与一个角为30°的直角三角板ABC拼在一起组成如图所示的平面四边形ABCD,其中∠DAC=45°,∠B=30°.若
| DB |
| DA |
| DC |
A、2
| ||
B、
| ||
| C、2 | ||
D、2
|
考点:向量在几何中的应用
专题:综合题,平面向量及应用
分析:不妨取DA=1,则DC=1,AC=
,AB=2
,BC=
.可得xB=DA+ABcos75°,yB=ABsin75°,再利用共面向量基本定理即可得出.
| 2 |
| 2 |
| 6 |
解答:
解:如图所示,
不妨取DA=1,则DC=1,AC=
,AB=2
,BC=
.
∴xB=DA+ABcos75°=1+2
×
=
,yB=ABsin75°=
+1.
∴B(
,
+1).
∴
=
+(
+1)
∴x=
,y=
+1,
∴xy=3+
.
故选:B.

不妨取DA=1,则DC=1,AC=
| 2 |
| 2 |
| 6 |
∴xB=DA+ABcos75°=1+2
| 2 |
| ||||
| 4 |
| 3 |
| 3 |
∴B(
| 3 |
| 3 |
∴
| DB |
| 3 |
| DA |
| 3 |
| DC |
∴x=
| 3 |
| 3 |
∴xy=3+
| 3 |
故选:B.
点评:本题考查了共面向量基本定理、含30°与45°角的直角三角形的性质,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
平面α与平面β平行的条件可以是( )
| A、α内有无穷多条直线与β平行 |
| B、直线a∥α,a∥β |
| C、直线a?α,直线b?β,且a∥β,b∥α |
| D、α内的任何直线都与β平行 |
椭圆
+
=1上的长轴长是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、5 | B、4 | C、10 | D、8 |
三棱锥S-ABC的4个顶点和6条棱的中点共有10个点,其中4点共面有m组,从m组中任取一组,取到含点S组的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
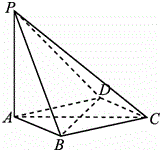 如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°. 如图程序框图表示求
如图程序框图表示求